密码算法侧信道分析

2024-05-08

Crypto

5.1k 词

这学期选了一门叫《硬件安全设计与检测》的课，本以为是研究固件或者Iot安全（其实这个也很有趣），没想到居然是讲密码算法侧信道分析的，这是科研级别的内容，有个专门的研究领域。通过物理手段分析密码算法，听起来就很离谱，实际上也确实如此。听过才知道，侧信道这领域比想象的要复杂和有趣得多。

密码学与侧信道分析

密码学分为两个大类：密码编码学与密码分析学。前者其实就是离散数学的应用，研究如何构造高效安全的密码算法。例如基于大素数分解困难的RSA不对称加密算法，或者DES对称密码算法。后者则是反过来，研究如何对现有的密码算法做攻击，根据掌握信息的多少又分为唯密文攻击、选择明文攻击等各种分类。攻防两端相互矛盾又相互促进。

侧信道分析就属于密码分析学，而且大概是其中最不讲理、最乱来的一个。密码分析学的大部分工作都在与数学打交道，侧信道分析则完全不同，它的基础建立在一条简单的原理上：

无论何种密码算法，都一定要运行在某种硬件环境中。

而一切硬件，都会在运行时，根据输入输出数据的不同而泄露不同的物理信息，例如时间，功耗和电磁辐射。

如果这种物理信息能建立起与密码算法执行指令IO的联系，就能反过来推导出密钥。

密码学的基本原理是科尔切夫假设：一切安全都蕴含在密钥之中。如果能够通过侧信道分析建立物理信息与密钥的相关性模型，反推出密钥，密码算法的安全性自然无从谈起，那便是密码分析学的成功了。

所谓的侧信道，其实就是正常通信的硬件之前的信息通路，也就是泄露的物理信息。其中这种分析思路在密码算法以外也有应用，例如使用高精度红外线分析仪，对ATM机的密码按键做测量，就能通过上面残留的温度，以及各个按键之间的温度差异，推断出上一个人的密码。这操作确实很离谱，据说密码局的密码学家就说，搞侧信道这帮人就是在耍流氓hhh。

当然，对于运行密码算法的硬件来说，泄露的信息当然不像ATM机按键上的温度那样，清楚简单地就能建立起与口令的联系。无论是专门的密码IC还是现代CPU，结构都非常复杂，尤其对有操作系统的硬件来讲，噪声比真正的侧信道信息要多得多。

所以侧信道分析也是涉及学科最多也最复杂的领域之一：

首先需要计算机基础，要分析机器指令与硬件侧信道的联系，计算机组成原理，汇编语言和操作系统自然必不可少
其次是电子学基础，分析CMOS反相器的功耗和电磁辐射，没有模电数电可不行；
最后是密码学、信息论和概率论，因为获取到信息非常复杂，要拿到有效的推断，必须通过数理统计手段做数据处理。

当然，本文主要作为通识入门，不会严谨论证原理，详细内容可以参考科学出版社的《密码旁路分析原理与方法》。

所有涉及到的代码都是我调试过的，环境为Win10的VS2022，完整源码参见这个GitHub仓库。

计时分析

一般用户最容易获取，也最难以避免的侧信道泄露，就是时间信息。

任何程序只要在硬件上执行，就会根据编译成机器码指令的不同而有不同的执行时间。如果对密码算法执行流程有仔细的了解，就能通过分析输入的密钥执行时间差异推断出验证正确与否。

PIN码计时攻击

这是纯理论分析，最简单的实例就是PIN码验证：

// Function to validate PIN
int validatePIN(int pin[]) {
    // Example correct PIN
    int correctPIN[PIN_LENGTH] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; 
    for (int i = 0; i < PIN_LENGTH; i++) {
        if (pin[i] != correctPIN[i]) {
            return 0; // Incorrect PIN
        }
    }
    return 1; // Correct PIN
}

这是一个十位PIN码的验证程序实例，逻辑非常简单，就是比较int数组是否相同，当遇到不同的值时直接return结束循环，这种写法效率更好，但蕴含侧信道信息泄露的危险。

稍加思考就会发现：如果输入PIN码在第一位就验证失败，此时循环只会执行一次就return；而如果十位都正确，则要执行十次比较指令，通过分析不同输入PIN码的时间差异，就能对每位做枚举攻击，而且时间复杂度惊人得低，只有10 * 10 = 100次尝试，而不是穷举的10 ^ 10。

以上就是基于计时分析的侧信道攻击原理，很好理解，但究竟如何计时呢？

这个问题比看起来复杂。因为现代CPU在循环中执行一次比较指令，例如masm汇编中的test a,b指令，只需要非常短的时间就能完成，因此就算是第一位就错误与完全正确的时间差异，也非常非常短，现代CPU时钟都是GHz级别，因此时间差异是纳秒级的，大部分计时器都做不到这种精度的时间测量。

TimeGetTime多媒体计时器比C语言库提供的一般Timer精度更高，但最高精度仅为1ms；Win32 API提供的QueryPerformanceCount有更高的精度，能到达微秒级，但对于密码算法执行时间，仍然精度不够。

解决方法是用CPU内部时间戳计时器，即RDTSC指令，记录的是CPU上电以来经过的时钟周期数，精度非常高，能达到纳秒级别。

调用RDTSC需要用内联汇编，好在Windows下微软提供了相关库用起来很方便，Linux要复杂一点：

#include <cstdlib>
#include <stdint.h>

//  Windows
#ifdef _WIN32

#include <intrin.h>
uint64_t rdtsc() {
    return __rdtsc();
}

//  Linux/GCC
#else

uint64_t rdtsc() {
    unsigned int lo, hi;
    __asm__ __volatile__("rdtsc" : "=a" (lo), "=d" (hi));
    return ((uint64_t)hi << 32) | lo;
}

#endif

但是问题也接踵而来。因为记录的数据精度非常高，而精度高的另一面就是：数据稳定性很差，受各种因素影响很大。所以对数据做统计处理很重要，否则几乎无法得出有效的推断，我用简单的重复测试取平均做了测试，效果比较差：

#define PIN_LENGTH 10
#define TRY_TIMES 10000000

int main(void) {
    int pin[PIN_LENGTH];
    int correct[PIN_LENGTH] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
    int incorrect[PIN_LENGTH][PIN_LENGTH] = {
        { 0, 2, 3, 4, 5, 6, 7, 8, 9, 10 },
        { 1, 0, 3, 4, 5, 6, 7, 8, 9, 10 },
        { 1, 2, 0, 4, 5, 6, 7, 8, 9, 10 },
        { 1, 2, 3, 0, 5, 6, 7, 8, 9, 10 },
        { 1, 2, 3, 4, 0, 6, 7, 8, 9, 10 },
        { 1, 2, 3, 4, 5, 0, 7, 8, 9, 10 },
        { 1, 2, 3, 4, 5, 6, 0, 8, 9, 10 },
        { 1, 2, 3, 4, 5, 6, 7, 0, 9, 10 },
        { 1, 2, 3, 4, 5, 6, 7, 8, 0, 10 },
        { 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 },
    };

    int i = 0;
    unsigned long sum = 0;

    while(i < TRY_TIMES) {
        //readPIN(pin);
        uint64_t tick = rdtsc();  // tick before
        validatePIN(correct);
        uint64_t end = rdtsc();
        sum += tick - end;
        i++;
    }

    cout << "验证正确时执行时间平均为：" << sum / TRY_TIMES << endl;

    
    for (size_t j = 0; j < PIN_LENGTH; j++)
    {
        i = 0, sum = 0;
        while (i < TRY_TIMES) {
            //readPIN(pin);
            uint64_t tick = rdtsc();  // tick before
            validatePIN(incorrect[j]);
            uint64_t end = rdtsc();

            sum += tick - end;
            i++;
        }

        cout << "在第" << PIN_LENGTH - j << "位验证出错时执行时间平均为：" 
            << sum / TRY_TIMES << endl;
    }

    return 0;
}

在Win10的VS2022下测试：

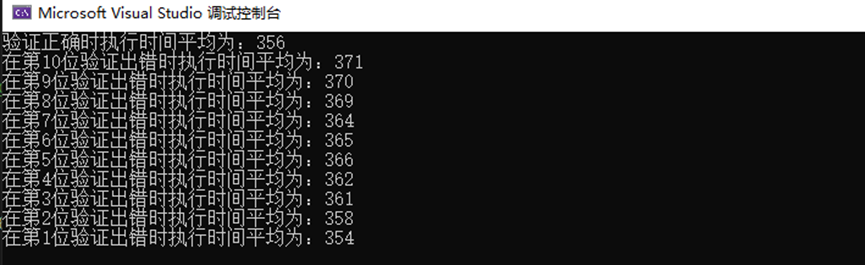
Kali Linux下用g++编译测试：

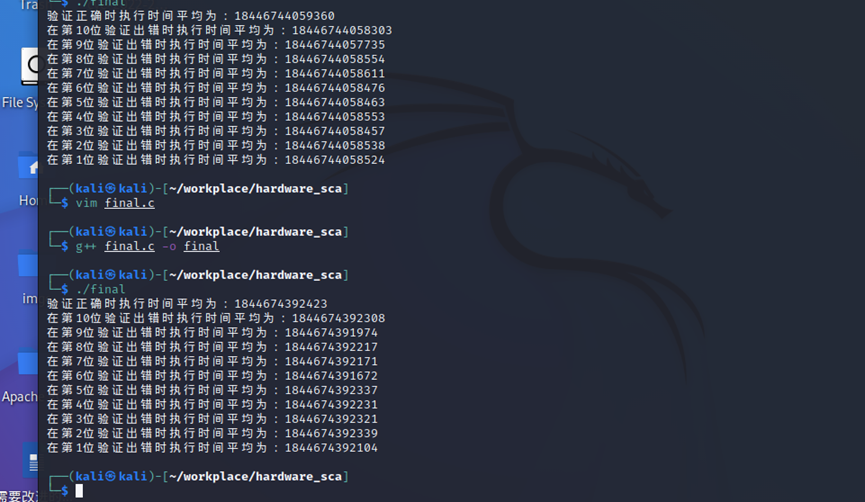
只能勉强看出符合理论。

RSA计时攻击

RSA是第一个不对称密码算法，密码学历史上最重要的算法之一。基于大素数分解困难的设计简洁优美，非常迷人。

RSA的核心是模幂运算，手算的话有欧拉定理和费马小定理（其实和前者一样）可以用，但计算机内部实现当然不能这么算。底层是利用取出幂的二进制数做平方乘算法实现的，将高次模幂拆解成了一系列乘法和平方运算，所谓的蒙哥马利算法就是对这种算法的优化实现。

平方乘的代码实现有两种写法，分别称为RL算法和LR算法，其实效率差别很小：

LR模幂运算：

uint64_t mod_pow_LR(uint64_t a, uint64_t b, uint64_t m) {
    uint64_t res = 1;
    while (b > 0) {
        if (b & 1) {
            res = (res * a) % m;
        }
        a = (a * a) % m;
        b >>= 1;
    }
    return res;
}

RL模幂运算：

uint64_t mod_pow_RL(uint64_t a, uint64_t b, uint64_t m) {
    // a为底数，b为指数，m为模数
    uint64_t res = 1;
    while (b > 0) {
        if (b % 2 == 1) {
            res = (res * a) % m;
        }
        a = (a * a) % m;
        b /= 2;
    }
    return res;
}

分析：可以看出算法对比特位为 0 和 1 时所做的操作不同，被2整除余1时二进制最后一位为1，此时多做了一步模乘运算，与为0时有时间差异，所以可以基于此对幂数（即RSA算法的密钥）做计时攻击。

与PIN码验证不同，RSA计时攻击需要生成大量随机的底数，并且需要对随机数做去重复：

// 生成n个用于测试的底数，指数和模数
void generate_test_base(int n)
{
    FILE* fp = fopen("test.txt", "w");
    if (fp == NULL) {
        cout << "Error opening file.\n";
        return;
    }

    // 设置随机数种子
    srand(time(NULL)); // 使用当前时间作为种子

    // 标记出现过的底数数组
    uint64_t bases[256] = { 0 };

    for (size_t i = 0; i < n; i++)
    {
        uint64_t base = (uint64_t)rand() % ((uint64_t)1 << 32);
        
        // 判断是否重复，重复则重新生成
        size_t j = 0;
        while (bases[j] != 0)
        {
            if (bases[j] == base)
            {
                base = (uint64_t)rand() % ((uint64_t)1 << 32);
                // 再次检查新生成的是否重复
                j = 0;
            }
            else 
            {
                j++;
            }
        }

        bases[i] = base;
        uint64_t exponent = (uint64_t)rand() % ((uint64_t)1 << 32);
        uint64_t modulus = (uint64_t)rand() % ((uint64_t)1 << 32) + 1;

        test_data[i].a = base;
        test_data[i].b = exponent;
        test_data[i].m = modulus;


        // 将测试用例记录在文件中
        fprintf(fp, "%llu %llu %llu\n", base, exponent, modulus);
    }

    fclose(fp);
}

之后进入实际的测试，攻击密钥的每个bit位。

按位取出幂数的bit位，然后分别赋值为 0 和 1，再分别计时计算多次。再对获取到的数据做统计分析，此处使用方差减少噪声：以实际运行时间为平均值，计算为 0 和为 1 时的方差，更小的说明与实际运行时间更接近，则推断为这一位的实际bit位数据：

// 攻击每个位
void attack_per_byte()
{
    int a = (int) test_data[0].a;
    int b = (int) test_data[0].b;
    int m = (int) test_data[0].m;
    cout << "测试数据：底数为" << a << " 幂数为" << b << " 模数为" << m << endl;

    // 使用RDTSC计时
    uint64_t start_time = rdtsc();
    mod_pow_LR(a, b, m);
    uint64_t end_time = rdtsc();

    uint64_t execution_time = (end_time - start_time);
    cout << "实际运行时间：" << execution_time << endl;

    int length = 64;
    double correct_rate = 0;
    for (size_t i = 0; i < length; i++)
    {
        int exponent_bit = get_bit(b, i);

        // 计算当第i位被赋值为0时
        clear_bit(&b, i);

        // 运行时间与实际时间的方差
        uint64_t data[100] = { 0 };
        for (size_t j = 0; j < 100; j++)
        {
            start_time = rdtsc();
            mod_pow_LR(a, b, m);
            end_time = rdtsc();

            data[j] = end_time - start_time;
        }

        double bit_value_0 = calculate_variance(execution_time, data, 100);
        cout << "当测试第" << i << "个bit为 0 时方差为：" << bit_value_0 << endl;
        
        // 计算当第i位被赋值为0时
        set_bit(&b, i);

        // 运行时间与实际时间的方差
        for (size_t j = 0; j < 100; j++)
        {
            start_time = rdtsc();
            mod_pow_LR(a, b, m);
            end_time = rdtsc();

            data[j] = end_time - start_time;
        }

        double bit_value_1 = calculate_variance(execution_time, data, 100);
        cout << "当测试第" << i << "个bit为 1 时方差为：" << bit_value_1 << endl;

        int check;
        if (bit_value_0 < bit_value_1)
        {
            check = 0;
            cout << "推断第" << i << "个bit为 0 ";
        }
        else
        {
            check = 1;
            cout << "推断第" << i << "个bit为 1 ";
        }

        cout << "====> 实际上第" << i << "个bit为 " << exponent_bit << endl;
        if (check == exponent_bit)
        {
            correct_rate++;
        }
    }

    cout << "正确率为：" << (correct_rate / 64) * 100 << "%" << endl;
}

推断比特位的正确率比想象要好一点，平均在50%左右：

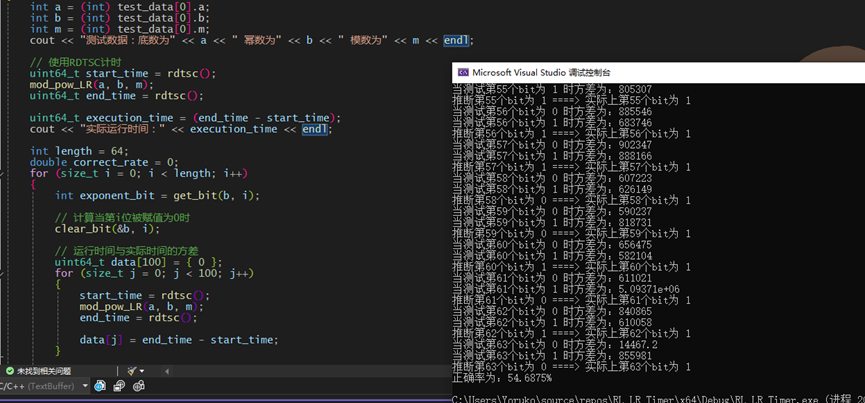
不过这种程度还是没办法推算出来密钥的，实际应用需要更精密的计时分析，但对于理论分析已经足够。

功耗/电磁分析

原理分析

基本公理：可编程器件只要执行指令，就会有许多个门电路不断翻转，具体的硬件实现就是CMOS反相器，通过分析CMOS的电磁辐射与功耗，就能反过来推出执行的指令和输入的数据。

与前面的计时分析不同，一般用户很难获取到精确的电磁辐射和功耗信息。在之前，不用特地设备，获取到CPU功耗是不可能的，但在现代intel x86CPU上，内置了一个功耗收集器，如果有办法获取到这个指令，就能收集到比外部仪器测量更高精度的功耗信息。

不过我简单查了下，与之相关的资料很少，所以方便起见，就用基于汉明重量模型的模拟值作为后面分析用的功耗信息。

与计时分析不同，基于功耗的侧信道分析，很难建立起具体功耗值与执行指令的联系（也就不会针对特定的密码算法），但很适合建立功耗与数据位（即0或者1）的联系，比计时攻击更适合用来推断密钥值。所以首要任务是：通过建立某种信息泄露模型，将功耗与数据比特位联系起来。常用的模型有汉明重量，汉明距离等。

我们本次实例使用汉明重量模型，其实非常简单：数据中所有的1加起来，就是这个数据的汉明重量值。

通过汉明重量模型将数据抽象化之后，需要测量收集与之对于的功耗值，再通过统计手段分析二者的相关性，就能推断出具体的数据，例如密钥。根据处理数据的统计方式不同，可以分成SPA，CPA，DPA等不同分析方式。

总结起来，功耗分析分为两个阶段：

测量阶段：建立泄露信息模型，对数据做模型化处理，收集功耗；
攻击阶段：对获取的数据做统计分析，推断密钥。

DES算法S盒功耗攻击

要实现的任务：

攻击对象：DES的一个Sbox

其中sbox是des中的6入4出的s盒子，C和K是6bit数，Sout是4bit的数。

要求：已知C的值和Sout（c，k）对应的信号值（自己仿真获得），攻击K。

泄露模型使用汉明重量模型。

分别用DPA和CPA实施攻击。

DES的S盒压缩实现

计算S1（B）的方法是：通过明文与轮密钥异或得到S盒输入B，将B的第一位和最后一位组合起来的二进制数决定一个介于0和3之间的十进制数（或者二进制00到11之间）。设这个数为i，B的中间4位二进制数代表一个介于0到15之间的二进制数（二进制0000到1111）。设这个数为j。查表找到第i行第j列的那个数，这个是一个介于0和15之间的数，并且它是能由一个唯一的4位区块表示的。

因为没有测量设备，所以使用汉明重量乘5作为获取到功耗的模拟值，C语言实现S盒输出函数：

int Sboxout(int num, int Nkey, int i) 
{
    // S盒输入的num为6bit，对其做位操作
    int bits[6];
    getPerBit(num, bits);

    int HW = 0;
    int P = 0;
    
    /// 拼凑出横纵坐标，做S盒查表替换
    int y = bits[0] + bits[5];
    int x = bits[1] + bits[2] + bits[3] + bits[4];

    // S盒输出
    int Snum = S_Box1[y][x];
    Sout[Nkey][i] = Snum;

    // 计算S盒输出密文的汉明重量
    HWw[Nkey][i] = HWFun(Snum);

    // 明文转为二进制
    std::bitset<sizeof(int) * 8> binaryNumber(mingwen[i]);
    std::string binaryString = binaryNumber.to_string().substr(sizeof(int) * 8 - 6);

    // 模拟测量到的功耗
    Ptest[Nkey][i] = HWw[Nkey][i] * 5;
    P = HWw[Nkey][i] * 5;
    
    cout << i << "\t" << mingwen[i] << "\t" << binaryString << "\t\t" << Snum << "\t" << HWw[Nkey][i] << "\t" << P << endl;
    
    // 当测试到正确密钥时，将功耗和汉明重量向量赋值给正确的数组
    if (Nkey == 43) {
        Pstd[i] = P;
        HWstd[i] = HWw[Nkey][i];
    }

    return Snum;
}

测量阶段

选取随机数量明文和设定好的正确密钥进行异或，作为模拟模型的中间值函数，得到的6bit结果作为S盒的输入，再选用汉明重量(HW)模型做仿真，S盒的输出需统计其中值的二进制中1的个数，作为汉明重量，所有输出得到一个汉明重量数组：

int HWFun(int num) {
    int count = 0;

    if (num == 0)
        return 0;

    while (num > 0)
    {
        // n &= (n – 1)能清除最右边的1
        // 因为从二进制的角度讲，n相当于在n - 1的最低位加上1
        num &= (num - 1);
        count += 1;
    }

    return count;
}

攻击阶段

需要遍历密钥的所有可能，因为轮密钥长度实际为6bit，因此只有0~63共64种可能。每次遍历都需经历测量阶段，最后得到所有猜测密钥的汉明重量数组。此时有两种方式做统计分析，分别是CPA和DPA：

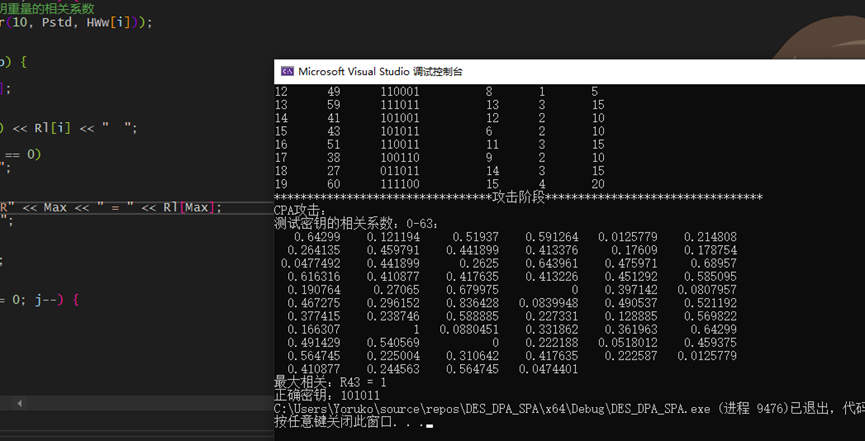
CPA

CPA(相关能量分析)攻击是一种对密码芯片的泄漏功耗进行统计分析而恢复密钥的攻击方法。DPA攻击的方法是对大量的曲线样点进行功耗统计测试，即根据大量功耗样本来分析密钥的值，它具有比简单功耗攻击更高的强度。

为让每个密钥猜测的汉明重量数组都与正确密钥得到的汉明重量数组共同计算Perason相关系数数组:

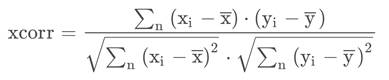
其中相关系数最大为正确密钥。实现：

double Corr(int n, int Pstd[], int Ptest[]) {
    // 返回两个向量数组的相关系数值
    double fenzi = 0.0;

    // 求两个数组的均值
    double PstdMean = meanNum(n, Pstd);
    double PtestdMean = meanNum(n, Ptest);

    double fenmu1 = 0.0;
    double fenmu2 = 0.0;
    double corr = 0.0;

    for (int i = 0; i < n; i++) {
        fenzi += (Pstd[i] - PstdMean) * (Ptest[i] - PtestdMean);
        fenmu2 += (Ptest[i] - PtestdMean) * (Ptest[i] - PtestdMean);
        fenmu1 += (Pstd[i] - PstdMean) * (Pstd[i] - PstdMean);
    }

    corr = fenzi / (sqrt(fenmu1) * sqrt(fenmu2));

    return corr;
}

CPA具体攻击实现：

double temp = 0.0;
for (int i = 0; i < 64; i++) {
    // 计算测试数组汉明重量的相关系数
    Rl[i] = abs(Corr(10, Pstd, HWw[i]));
        
    // 找出最大的值
    if (Rl[i] > temp) {
        Max = i;
        temp = Rl[i];
    }
        
    cout << setw(10) << Rl[i] << "  ";
        
    if ((i + 1) % 6 == 0)
        cout << "\n";
}
    
cout << "\n最大相关：R" << Max << " = " << Rl[Max];
cout << "\n正确密钥：";
    
int bit[6];
getPerBit(Max, bit);

// 打印出正确的密钥
for (int j = 5; j >= 0; j--) {
    cout << bit[j];
}

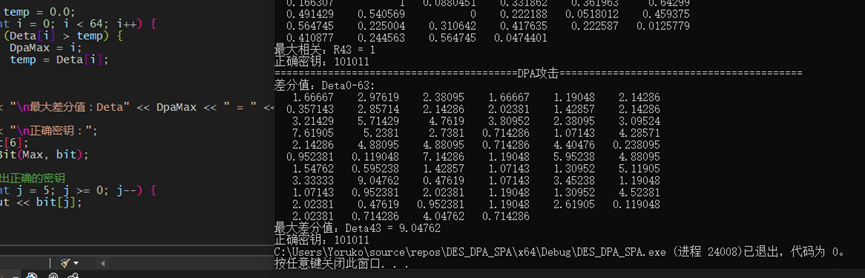
DPA

DPA(差分能量分析)是将密钥猜测的汉明重量数组与正确的数组做差分计算，正确密钥得到的汉明重量数组划分成两个集合，分别计算均值，再相减得到的差值最大为正确的密钥:

void Dpa() {
    //以2为界
    int Larr[20];
    int Harr[20];
    int Lc = 0;
    int Hc = 0;

    for (int i = 0; i < 20; i++) {
        if (HWstd[i] < 2) {
            Larr[Lc] = i;
            Lc++;
        }
        else {
            Harr[Hc] = i;
            Hc++;
        }
    }

    for (int i = 0; i < 64; i++) {
        int Htemp = 0;
        int Ltemp = 0;

        //HW小于2,对应累加
        for (int j = 0; j < Lc; j++) {

            Ltemp += Ptest[i][Larr[j]];
        }
        //HW大于2，对应累加
        for (int j = 0; j < Hc; j++) {

            Htemp += Ptest[i][Harr[j]];
        }

        DpaP[i][0] = Ltemp * 1.0 / Lc;
        DpaP[i][1] = Htemp * 1.0 / Hc;
        Deta[i] = abs(DpaP[i][0] - DpaP[i][1]);

    }

    cout << "\n=========================================DPA攻击=========================================\n差分值：Deta0-63:\n";
    for (int i = 0; i < 64; i++) {
        cout << setw(10) << Deta[i] << " ";
        if ((i + 1) % 6 == 0) {
            cout << "\n";
        }
    }

    double temp = 0.0;
    for (int i = 0; i < 64; i++) {
        if (Deta[i] > temp) {
            DpaMax = i;
            temp = Deta[i];
        }
    }

    cout << "\n最大差分值：Deta" << DpaMax << " = " << Deta[DpaMax];

    cout << "\n正确密钥：";
    int bit[6];
    getPerBit(Max, bit);

    // 打印出正确的密钥
    for (int j = 5; j >= 0; j--) {
        cout << bit[j];
    }
}

测试得到的结果相当漂亮，DPA和CPA都成功推断出了正确密钥：

Cache分析

这个部分最复杂，但也最有意思。

但是我懒得仔细写了，关键是两个经典的CPU漏洞：幽灵和熔断。其实是一个原理，核心利用点如下：

现代处理器的分支预测
cache命中与失效的差异
cache更新机制的懒加载

所以把这个漏洞称为”高性能的代价”相当合适wwww

标签

归档

最新文章