第八章 多元函数微分
多元函数极限
与一元的关键区别:
- (x,y)可以以*任意方式(即沿任意路径)*逼近(x_0,y_0),此时满足这个条件才能称为多元函数极限存在。
- 连续不一定可导,可导也不一定连续
与一元相同:
- 局部有界
- 保号性
- 有理运算法则
- 极限与无穷小的关系:无穷小乘有界函数还是无穷小很常用
- 夹逼原理
注意:洛必达不能用于多元极限
求多元极限(一般比较简单)
如果是分式极限且x,y均趋近于0,可以直接看分子分母的次数判断极限:
- 分子次数大于分母:0
- 分子等于分母:不存在
- 分子小于分母:无穷大
判断之后,一般用两种方法证明:
- 取绝对值|f(x,y)|,构造绝对值不等式,再用夹逼原理
- 分离变量,用无穷小乘有界函数仍然是无穷小
判断多元极限不存在的方法
直接取y=kx,代入计算极限,化简到最后如果有k,则说明极限随k值选取变化,即多元函数极限不存在。
多元函数的连续性
概念: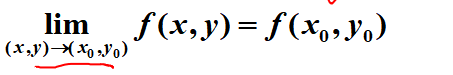
与一元函数不同的最大值定理:有界闭区域D(一元是闭区间)上的连续函数,在区域D上必然能取得最大最小值。
偏导数
一元函数导数有两种定义: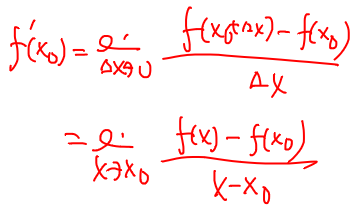
二元函数的偏导数同样有类似的两种定义,根据题目条件选择。
Δx为自变量的定义:
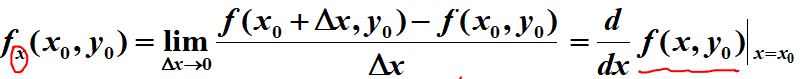
在要求的点函数不存在/不连续时,需要用定义求偏导。
注意:如果求f(x,y)在(0,0)处对x的偏导,实际上是将y看作常数,求一元导数,因此可以直接将y=0代入f(x,y),方便用定义求偏导。
0极限:对0/x,在x趋近于0时,极限仍然为0
因为0可以看作是最高阶的无穷小,比任何趋近于0的无穷小更高阶,因此为0
偏导数的意义:对x偏导,即f(x,y)在x轴方向上(即y=y_0直线上)的变化趋势;反之对y求偏导,则是多元函数在y轴方向上的变化趋势。
例如已知对f(x,y)对x的偏导在某区间上大于0,且对y的偏导在区间上小于0,则函数沿x轴方向上单调增,沿着y轴方向单调减(沿y轴负方向增加)。
高阶偏导
对高阶偏导,结果与先对x求偏导还是先对y无关: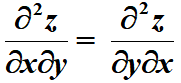
全微分
定义:若Δz = f(x_0+Δx, y_0+Δy) - f(x_0, y_0) = AΔx + BΔy + o(p), p=sqrt(Δx^2+Δy^2),则称函数在(x_0,y_0)处可微,全微分dz = Adx + Bdy。
- 可微的必要条件:偏导数存在
即函数在某点可微,则该点处的所有偏导数一定存在: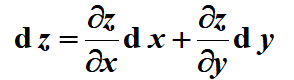
即与一元函数不同:可微可以推出可导,但可导推不出可微。
- 可微的充分条件:偏导数存在,且偏导数连续
但是可微也推不出偏导数连续
定义判断可微性

b)方法:实际上是利用全微分定义:Δz = AΔx + BΔy + o(p),其中0(p)是p的高阶无穷小,因此可以推出:
Δz - (AΔx + BΔy) 是 p的高阶无穷小,因此凑成上面的分式取极限时为0.
当然Δx和Δy形式都可以变,只要满足取极限即可。
连续、可偏导与可微的关系
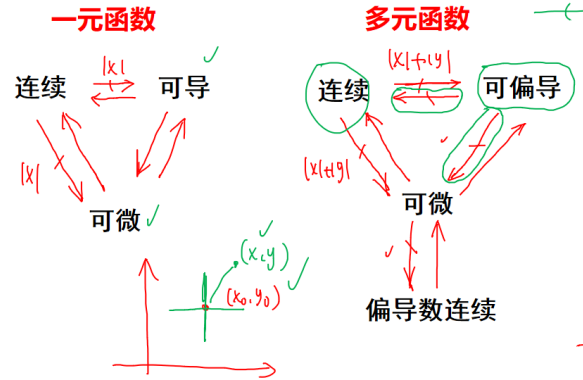
注意连续与可偏导是既非充分条件也非必要条件。
实际上可偏导推不出可微很直观:因为偏导仅仅标识函数在两个方向(x轴和y轴方向)上的变化趋势,但可微要求函数在任意路径上的变化趋势都存在。
经典反例

多元函数微分
复合函数偏导/全微分
一元函数求复合函数导数很直观:如y=f(u),u=g(x)均可导,则有
$$
y_x’ = y_u’ u_x’ = f’(u) g’(x)
$$
复合函数求偏导:对多元函数,复合函数要有偏导,需要内层函数可导,且外层函数有连续偏导,才能求。(但对一元函数,只需要内外层函数均可导即可)。

首先要确定变量之间的关系,然后画出变量树形图即可。
注意:对于一阶复合偏导很容易,但二阶复合求偏导时,很容易漏项,例如对
$$
y=f(e^x,\cos x)
$$
求二阶偏导。一阶偏导很容易求:
$$
\frac{dy}{dx} = f_1’e^2+f_2’(-\sin x)
$$
f_1’为将e^2看作v,再对v相对于y函数,求v的偏导,f_2’类似。求二阶偏导时,再对上面的式子相对于x求偏导:
$$
\frac{d^2y}{dx^2} = f_{11}’e^2e^2 + f_1’e^2 + … ()
$$
此时出错!因为对f_1’*e^2求偏导时,f是e^2和cosx的函数,则f_1’也是这两项的函数,因此对f_1’求导时,也要像一阶时一样,分别对这两项复合求偏导:
$$
\frac{\part f_{1}’}{\part x} = f_{11}’’*e^x + f_{12}’’ * (-\sin x)
$$
代入上面的(*)式:
$$
\frac{d^2y}{dx^2} = f_{11}’e^2e^2 + f_1’*e^2 + f_{12}’’e^x(-\sin x) + …
$$
这个才是正解。
另外,在求二阶偏导时,如果形式很复杂,可以在求出一阶偏导之后用“先代后求”简化为一元函数。
注意2:在求复合函数的偏导时,如果是z = xf(u) + yg(v)的形式,令z=F(x,y),则有z/x和F/x两种偏导,既有:
$$
\frac{\part z}{\part x} = \frac{\part F}{\part x} + \frac{\part F}{\part u} * \frac{\part u}{\part x}
$$
在计算F/x偏导时,将u和v都看做与x无关的常数,即上面的示例z=F(x,y)中,F/x偏导为f(u)。
全微分形式不变性
对一元复合函数,如对y=f(u),u=g(x)均可导,则有:
$$
dy = y_x’dx = y_u’u_x’dx = y_u’du
$$
此时可以发现dy既可以表示为y_x’dx,也可以写为y_u’du,形式相同,因此有微分形式不变性。
对全微分也有类似结论: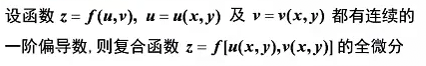
但是要保证所有函数都可微,因此条件加强了。
具体形式也与一元类似: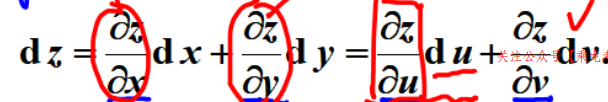
隐函数偏导/全微分
由方程F(x,y)=0确定的隐函数y=y(x),求这个函数的导数此时有:
$$
y’ = -\frac{F_x’}{F_y’}
$$
对多元函数也是类似:

还有其他方法:
- 直接对F(x,y,z) = 0两边求导,即可得到
$$
F_x’ + F_z’\frac{\part z}{\part x} = 0
$$
- 利用全微分形式不变性:对F(x,y,z)=0两边求全微分
$$
F_x’dx+F_y’dy+F_z’dz=0
$$
$$
dz=z_x’dx+z_y’dy
$$
此时求出dz的两个系数即得到函数偏导。
这种方法的主要优势是不需要分析变量之间的关系,直接求全微分,然后把要求的dz/dx形式凑出来即可。
注意:在使用代公式求F_x’和两边求导时,z与x的关系不同。
代公式F_x’/F_z’时,z看作与x无关的常数,即z’ = 0,因为对F=0求x的偏导,只有x一个变量
两边求导时,z看作x和y的函数,即出现z时,两边对x求导得:
$$
z’= \frac{\part z}{\part x}
$$
同理两边对y求导时:
$$
z’= \frac{\part z}{\part y}
$$
多元函数极值

无约束极值
与一元的定义几乎相同:

必要条件

注意:此时两个偏导均为0时称该点为驻点,但不一定是极值点。
极值点与驻点的关系:没有关系,互相不能推导。
反例:
- 是驻点不是极值点:f(x,y) = xy的(0,0)点
- 是极值点不是驻点:f(x,y) = |x| + |y|的(0,0)点取极小值,但两个偏导都不存在
但对可导函数:极值点一定是驻点。
可能出现的极值点:
- 驻点
- 偏导均不存在,或者某个偏导不存在,存在的偏导等于0
充分条件

条件极值与拉格朗日乘数法
条件极值:求函数f(x,y)在g(x,y)条件下的极值
几何意义: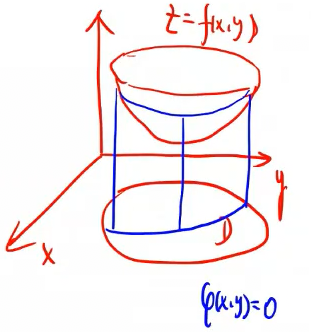
原本是在定义区域D内取极值,现在是在曲线(即f与g两个曲面的交线)上取极值。
拉格朗日乘数法: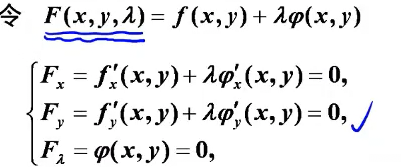
如果给出的约束条件是简单图形,例如x^2+y^2/4<=1为椭圆,求最值时,可以化有条件为无条件。
此时只需要求出驻点,(在区域内部时)代入驻点求二元函数值;然后求边界处的函数值(即把约束条件代入给出的二元函数)再做比较即可。
也可以把直角坐标系转为参数方程再化条件为无条件(即代入)。
最大最小值

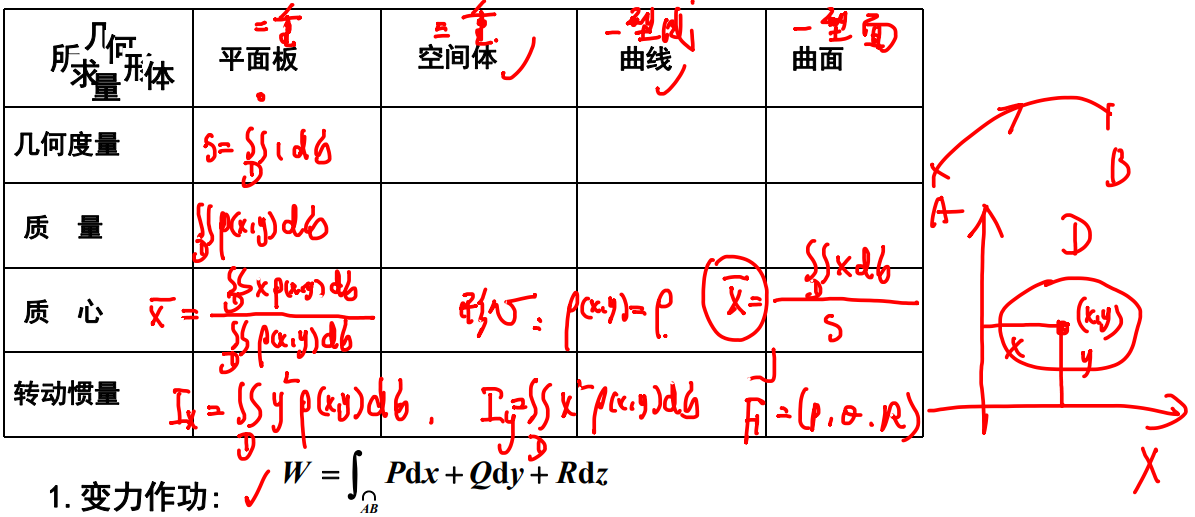
第九章 二重积分

概念与性质
定义: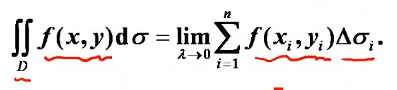
几何意义:在区域D上,函数z=f(x,y)曲面投影下的体积。
性质
- 不等式性质:
- 在D上有f(x,y)<g(x,y),则在D上的二重积分也有F<G。
- 若在D上有m <= z(x,y) <= M,则有:
$$
m*S \leqslant \iint_Df(x,y)d\sigma \leqslant MS
$$
S为区域D的面积。
- 绝对值不等式:
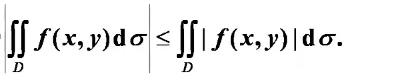
- 积分中值定理

与一元中值定理完全对应,只是长度换为区域面积。
二重积分计算
直角坐标
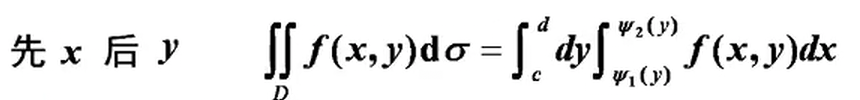
极坐标
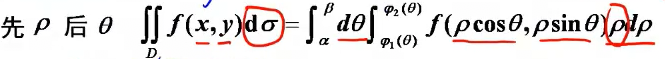
判断什么时候适合极坐标:
函数:
$$
f(\sqrt{x^2+y^2}) 、f(\frac{x}{y})、f(\frac{y}{x})
$$积分区域:
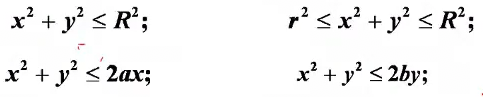
主要用在积分区域是圆的情况,如果圆心不在原点或坐标轴,可以先平移再用极坐标。
利用对称性和奇偶性

即如果区域D关于x轴对称,则看函数是否关于y是奇函数,是则为0,为偶函数则可以用积分区域一半再乘二计算;反之关于y轴对称,则看函数是否关于x有奇偶性。
利用变量对称性(常用)
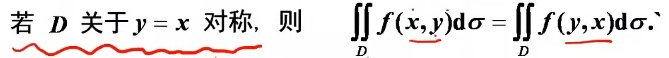
注意:实际上是区域D的对称性

这个式子是通用的,但D对称时有D(x,y) = D(y,x).
尤其对积分区域是圆时,很常用。
例如D为圆,积分函数为x^2-y,则对y在D上的二重积分为0,即转化为^2,同时D关于y=x对称,因此x^2的二重积分等于y^2,即原式 = 1/2(x^2 + y^2)的二重积分,再化为极坐标就很容易计算了。
另外:如果是x/(x+y)的类型,也可以转化为1/2*(x+y)/(x+y)来消掉分母。
图像
常用函数图像。
|x| + |y| <= pi/2的图像: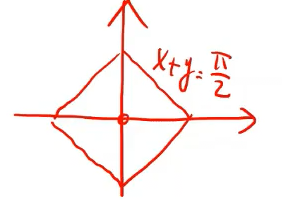
还有x^2/3 + y^2/3 = a^2/3
或者写成x = acos^3t,y = asin^3t,均为星型曲线: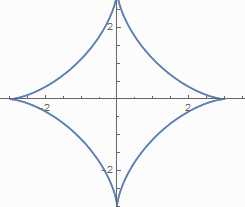
含绝对值
对有绝对值的函数求定积分或者二重积分,要注意分区间计算,即可去掉绝对值号。
例如如果积分区域有对称性,可以用上面的方法化为正数时计算再乘2或者乘4。
第十章 无穷级数

常数项级数
主要考察:常数项级数的敛散性判断
概念
定义: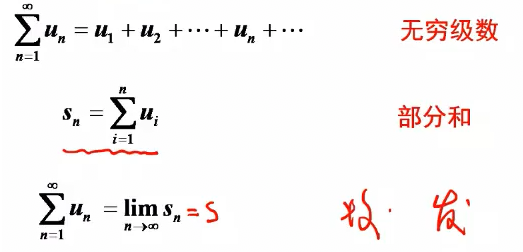
性质
- 若级数u_n收敛于s,则级数ku_n也收敛,并且收敛于ks;
- 若u_n于v_n分别收敛于m和n,则其逐项相加与逐项相减得到的级数分别收敛于m+n 和 m-n;
注意:收敛 ± 发散 = 发散;发散 ± 发散 = 不确定
- 在级数中去掉、加上或者改变有限项,对级数敛散性不影响(但如果级数收敛,则对收敛的极限有影响)。即前有限项不影响级数敛散性。
- 收敛级数加括号仍收敛,且其和不变。
注意:
- 原本级数收敛 ===> 级数加括号收敛 (反之不成立,例如1-1+1-1+1…加括号可以收敛,但本身不收敛)
- 加括号发散 ====> 原级数发散
- 级数收敛的必要条件:当n趋近于无穷时,u_n极限为0
但反之不成立,u_n极限为0,级数不一定收敛,例如调和级数Σ{1/n}就发散。
判断敛散性原则
正项级数
基本定理:正项级数如果收敛,则前n项和s_n一定有界。
因此可以推出比较判别法:
- 大的级数收敛,则小的级数一定收敛
- 小的级数发散,则大的级数一定发散
利用放缩判断即可:已知收敛 => 放大,已知发散 => 缩小。
!!注意:此处下面的所有判别法和上面的比较判别法都只能应用于正项级数。!!
比较审敛法极限形式
最常用的是第一条:如果n趋近于无穷,则u_n/v_n的极限是常数且不等于0时两个级数同敛散性。

比值法
直接做比值求极限,若小于1则收敛,若大于1则发散,等于1则不确定。
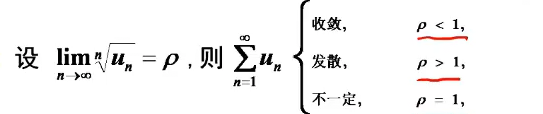
根式法
积分判别法(新增)

即将级数敛散性与反常积分敛散性联系起来,可以转为求反常积分求解。
两个常用级数(常用)
p级数和等比级数:

交错级数
即其中的项正负交错的级数。
判断交错级数敛散性:
反之不能成立,即如果交错级数收敛,u_n不一定单调减。
任意项级数
若绝对值级数收敛,则级数本身一定收敛,称为绝对收敛。

基本结论:
实际上上面的结论2,其实是条件收敛的级数,所有负项级数和所有正项级数都发散。
注意:经常需要将给出的级数拆为交错级数和正项级数方便判断
另外:在n趋近于无穷大时,n^n/(n+1)^不为1,而是为1/e
含绝对值的级数
常用结论:|a_n|级数收敛,则a_n^2级数也收敛。
原因很容易推导:|a_n|趋近于0,则|a_n|<1,则a_n绝对值一定大于a_n^2。大收敛推出小收敛。
但如果有a_n级数收敛,推不出a_n^2级数收敛,例如(1)^n/sqrt(n)。
幂级数

其中题型三最难,也最常考,实际上就是函数展开的逆过程。
收敛半径、收敛区间与收敛域
定义: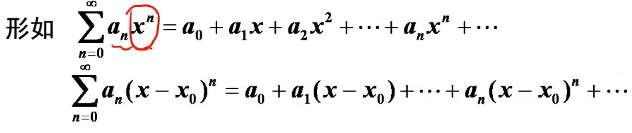
称为幂级数。
阿贝尔定理
(1) 若a_n*x^n级数在 x=x_0(x_0≠0) 时收敛,则在当|x| < |x_0|时幂级数绝对收敛。
(2) 若a_n*x^n级数在 x=x_0 时发散,则在当|x| > |x_0|时幂级数发散。
根据阿贝尔定理可以推出一个对称的区间,向内的区间是收敛区间,向外则是发散区间。(注意:收敛区间一定是开区间,不关心端点)
因此将该区间的一半长度称为收敛半径。
再考察收敛半径的端点是否收敛,即可判断收敛域。
因此求收敛域的关键就转化为求收敛半径。
在给出的幂函数为抽象a_n时,经常用阿贝尔定理判断收敛域,当给出的一个点有幂级数条件收敛时,该点必然收敛区间的端点(重要)。
幂级数收敛性的三种情况

实际上对应三种收敛半径:
- R = 正无穷
- R = 0
- R为常数
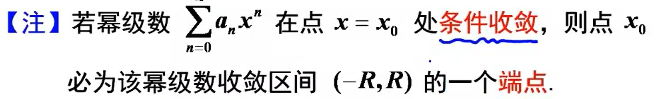
求收敛半径(常用)
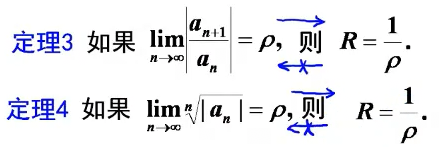
注意只能左推,不能右推。
实际上都是从前面的敛散性判断推得的。
一般定理4计算更简单:多用n的开n次方在n趋近于无穷大时为 1 这个常用极限。
注意:如果缺项,可以转化为x^n的几次方求。例如x^(2n+1)与x^2n相同,即(x^n)^2.
有绝对值时,可以提出其中最大的项,让绝对值内转为必为正。
性质
有理运算
若有幂级数a_n*x^n收敛半径为R1,另一幂级数b_n*x^n收敛半径为R2,令R=min{R1,R2}(即收敛区间的公共部分),当x属于(-R,R)时:
- 加减:级数相加减 = 各项相加减再取级数
- 乘法:级数相乘,等于各项相乘取级数(注意:相乘的各项需要下标相加为n)
- 除法:与乘法类似
分析性质
幂级数收敛半径为R,和函数为S(x),则有:
- 连续性:S(x)在收敛域上连续
- 可导:S(x)在(-R,R)【注意区间不包含端点】上可导,且可逐项求导,收敛半径不变。(可以连续使用)
- 可积:在收敛域上可积,且逐项可积分,半径不变化。
和函数与单项的关系
$$
\sum^{\infty}{x=1}u{n+1} = \sum^{\infty}{x=1}u{n} - u_1
$$
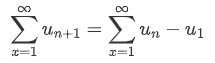
即u_n+1的和函数从2开始求和,比u_n少了第一项u_1。
函数的幂级数展开
f(x)在某点的邻域内,若能展开为幂级数,则其展开式是唯一的,即所谓泰勒级数。
泰勒级数收敛的必要条件:

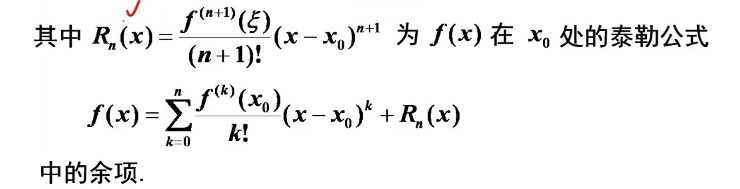
即考察泰勒公式的余项是否为0,即可得知能否展开为幂级数。
常用展开式:其中的区间为收敛区间
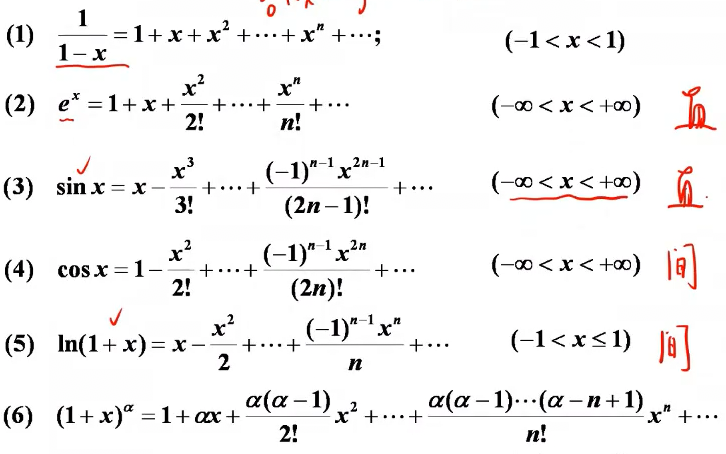
一般不直接展开,而是用现有展开式与幂级数性质间接展开。
注意:
- 在x_0处展开时,将公式中的x化为x - x_0.
- 如果形式复杂,可以先求导再求变上限积分(注意不是不定积分,否则还有常数C)简化式子。
- 要注意项数中包不包括第0项。
傅里叶级数

傅里叶系数
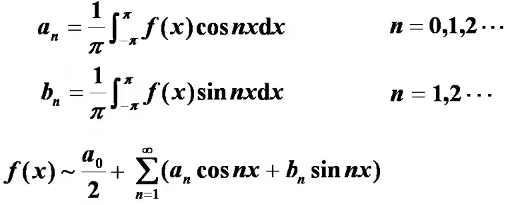
a_n,b_n称为傅里叶系数,可构成傅里叶级数——即f(x)展开为三角函数(但不一定可以展开)。
收敛定理

展开的要求比幂级数展开更低,幂级数要求任意阶可导,傅里叶级数甚至连续都不要求。
不连续时,函数收敛于“左端点的右极限 与 右端点的左极限”的平均值。
周期为2pi的函数展开

周期为2l的函数展开
在[-l,l]上展开:
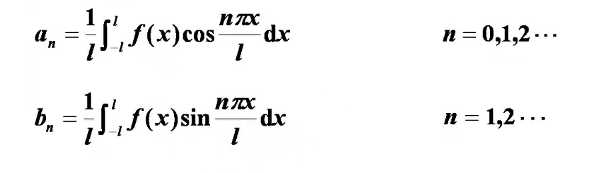
如果在周期有奇偶性:

奇函数时:只有正弦项;偶函数时:只有余项项。
在半个周期上展开时:

注意:在用收敛定理时,要先将半个周期扩展为一个周期。
第十一章 空间解析几何与多元微分的几何应用
向量代数
单位向量
向量 除以 向量的模。
数量积
得到的是一个数
两种表示:代数和几何表示
满足交换律与分配率
应用:求模、求夹角和判断两向量垂直
向量积
|a X b| = |a|*|b|*sinα 得到的是一个向量
方向:右手法则
代数表示: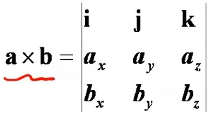
不满足交换律,满足结合律和分配律
几何应用:
- 求同时垂直a和b的向量:aXb
- 求以a和b为邻边的平行四边形的面积:S=|a X b|
- 判断两向量平行:a平行b,则aXb=0,且可以反推。
混合积
(abc) = (aXb)*c
代数表示: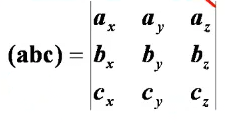
运算规律:
- 轮换对称性:(abc) = (bca) =(cab)
- 交换变号:(abc) = -(acb)
即轮换值不变,交互变负号
几何应用:
- V_平行六面体 = |(abc)|
- 判断三向量共面:(abc)= 0
空间平面与直线
平面方程
主要有三种写法:一般式,点法式,截距式
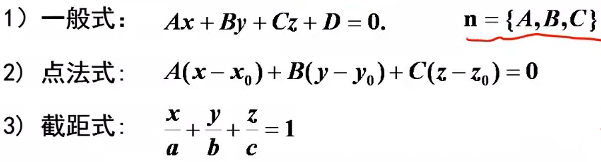
n为平面法向量。
直线方程
同样有三种:一般式,对称式,参数式
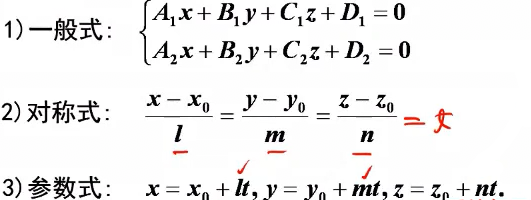
对称式可以写成参数式。
平面与直线的位置关系
主要有三种:平行,垂直,夹角
关键是:平面的法线向量和直线的方向向量
点到平面距离公式
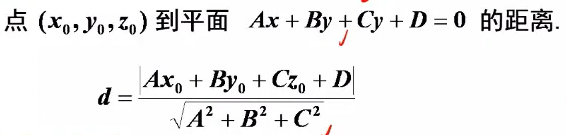
点到直线距离公式
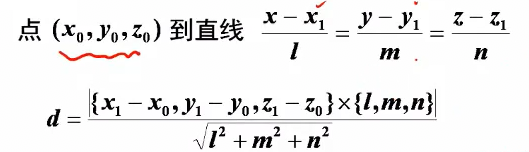
曲面与空间曲线
方程表示:
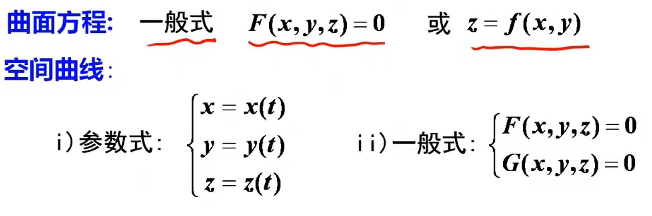
常用曲面
旋转面
最常见的是旋转面:
一条平面上的曲线绕平面上一条直线旋转。
例如L是yOz上一曲线,方程为f(y,z) = 0 && x = 0,则有:
- L绕y轴所得旋转面方程为:f(y, ±sqrt(x^2 + z^2)) = 0
- L绕z轴所得方程:f(±sqrt(x^2 + y^2), z) = 0
即绕谁转谁不动,将另一变量换为sqrt(x^2 + ..^)。
参数方程形式给出
当给出的为:
x = x(t)
y = y(t)
z = z(t)
其旋转曲面很容易得出,例如绕z轴旋转:
x = sqrt(x^2 + y^2) * cos
y = sqrt(x^2 + y^2) * sin
z = z(x)
即z不变,x和y变成sqrt(x^2 + y^2)再乘三角函数的形式。
柱面
平行于定直线,且沿特定曲线移动的直线L形成的轨迹,称为柱面。
有两种准线:
- 准线为平面直线,例如准线为f(x,y)=0 && z=0,求母线平行于z轴,此时直接消去z即得柱面。
- 准线为两平面交线,求母线平行为z轴的曲曲面,此时联立方程组消去z也可以得到柱面方程H(x,y)=0。
二次曲面(重要)
(1) 椭圆锥面:
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} = z^2
$$
但不常用,更常用的椭圆锥面的特例:圆锥面 x^2 + y^2 = z^2 
(2) 椭圆球面:
$$
\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1
$$
特殊情况即球面:x^2 + y^2 + z^2 = 1
其他几种情况一般不常用:

实际上只有旋转抛物面最常用。
空间曲线的投影
有曲线:F(x,y,z)=0 & G(x,y,z)=0,在xOy面上投影的曲线方程为:
H(x,y) = 0 && z = 0
即联立消去z(对x0y面投影而言),此时得到平面方程,再联立z=0即得投影曲线方程。(若有曲面中没有z,即在xOy面上,此时无需解直接将该曲线作为投影曲线)
注意:解出来投影曲线的方程之后,要注意范围
例如空间曲线是球面与包含在球面内的柱面的交线,此时在其中一个平面上投影曲线是
z^2 + ax = a^2,即是无限延伸的抛物线,需要限定范围。
多元微分在几何上的应用
实际上曲面求切平面的两种形式可以化为一种:
z = f(x,y) ==> f(x,y) - z = 0,对方程求偏导即得(f_x, f_y, -1).

其中n_1 = {F_x, F_y, F_z},n_2 = {G_x, G_y, G_z}.
注意:两曲面相交决定的曲线,其切向量同时垂直于两个平面的法向量。
第十二章 多元积分及其应用
三重积分
定义: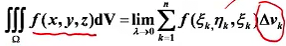
性质:
- 绝对值不等式
- 积分中值定理
与定积分一样。
计算
将三重积分化为先求二重积分,再求单个积分。
1. 先一后二
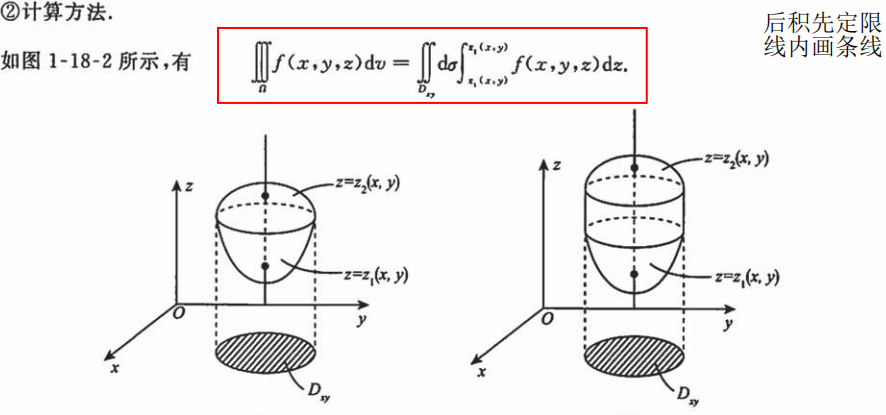
二重积分的积分区域就是三重积分区域在xOy面上的投影;
定积分区域:做平行于z轴的射线,交点表达式(即曲面表达式,z=f(x,y)即为上下限。
2. 先二后一
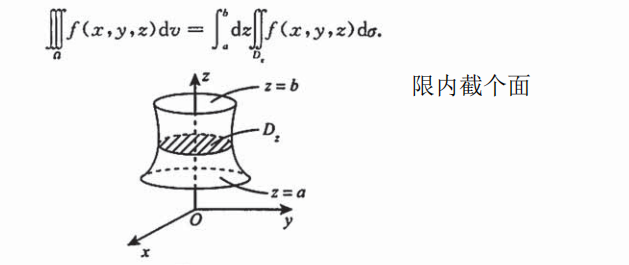
与二重积分类似,使用x = 0平面去截取积分区域(注意与上面的投影不同,有可能需要分界),获得的区域表达式和边界再求定积分。
适用场合:
- 函数:当被积函数是单个变量的函数时
- 区域:被积分区域为
旋转体时
柱坐标
x = r*cosα
y = r*sinα
z = z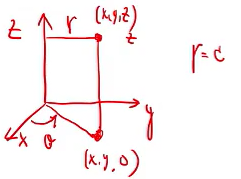
柱坐标计算三重积分:dv = r * dr * dα * dz,再代入x,y,z到被积函数即可。
适用于柱坐标计算的情况:
- 函数:g(z)*f(sqrt(x^2+y^2)) ====> g(z)*f(r)
- 区域:柱体,锥体
球坐标
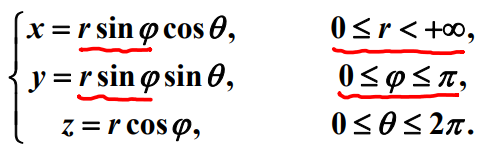
化为体积微元:dv = r^2 * sinφ * dr * dθ * dφ
适用于球坐标计算的情况:
- 函数:f(sqrt(x^2+y^2+z^2))
- 区域:球体、半球体、两个球面、球面和锥面
利用对称性和奇偶性计算
若积分区域关于xOy面对称,则有:
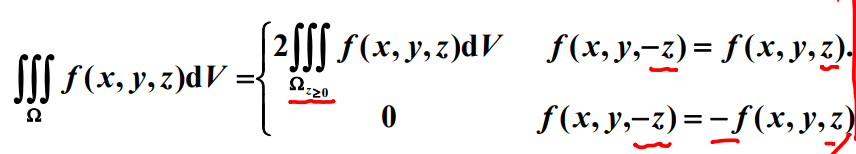
利用变量对称性
对积分区域为x^2 + y^2 + z^2 <= R^2的球面,此时三个坐标实际上地位等同。
因此有: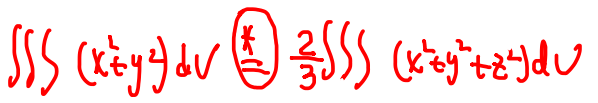
尤其适用于球面时的积分区域,之后可以用球坐标。
曲线积分
对弧长的曲线积分:第一类曲线积分
积分单元为弧长单元的变化量
定义: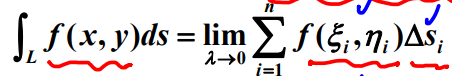
性质:对弧长的线积分与路径方向无关。
计算
实际上就是将弧长单元dS化为给出形式:
参数方程给出:
ds = sqrt(x'^2 + y'^2) * dt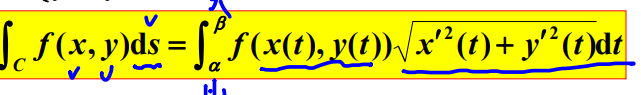
直角坐标给出:
ds = sqrt(1 + y'^2) * dx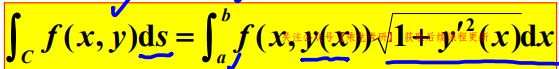
极坐标给出:
ds = sqrt(ρ^2 + ρ'^2') * dθ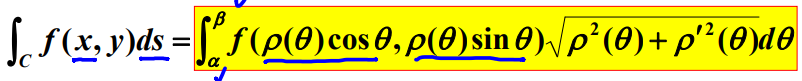
奇偶性
与二重积分完全相同:

对称性
若积分曲线关于直线y=x对称,则函数中自变量x和y互换,曲线积分不变
空间曲线时
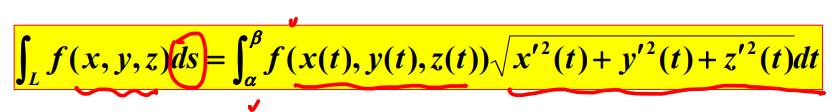
对坐标的曲线积分:第二类曲线积分
积分单元为坐标x和y的变化量。
定义: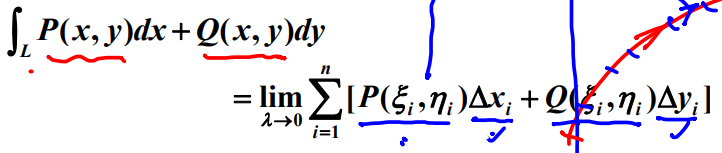
性质:与路径方向有关
计算:
- 参数方程:
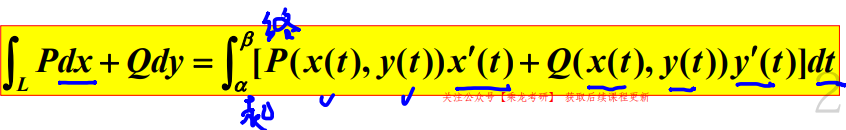
注意:定积分上下限是起始点和终点
格林公式
对于封闭曲线,可以用格林公式计算线积分:
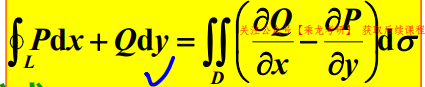
正向的定义:沿边界走,区域始终在左侧(即正向是相对于区域而言的)。
可以用补线将区域封闭(注意方向要回环),再用格林公式。
利用线积分与路径无关
判断定理:
单连通:区域内没有“洞”
方便计算:
- 改换路径:由曲线改为沿坐标轴的直线
- 利用原函数:
$$
\int_{(x_1,y_1)}^{(x_2,y_2)}Pdx+Qdy=F(x_1,y_1) - F(x_2,y_2)
$$
即Pdx + Qdy = dF(x,y)
求原函数方法:1. 偏积分 2. 凑微分(更常用)
注意:当偏微分分母有变量时,以此原点为界,都不能是单连通:
例如对P求y的偏微分,得1/y^3,此时积分与路径无关区域为y>0。
当区域非单连通时
可以使用在光滑曲线上做曲线积分Pdx + Qdy = 0,此时也可证明区域上线积分与路径无关。
选择方法
L封闭:格林公式
L不封闭:看曲线是否与路径无关,有关且难直接算时补线用格林公式。
两类线积分联系
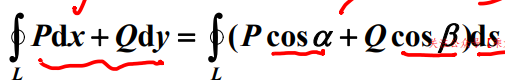
空间曲线时的计算法
求空间曲线参数方程时:
例如空间体与平面的交线:一般先求空间体的投影的参数方程,再代回平面求出z的参数方程。
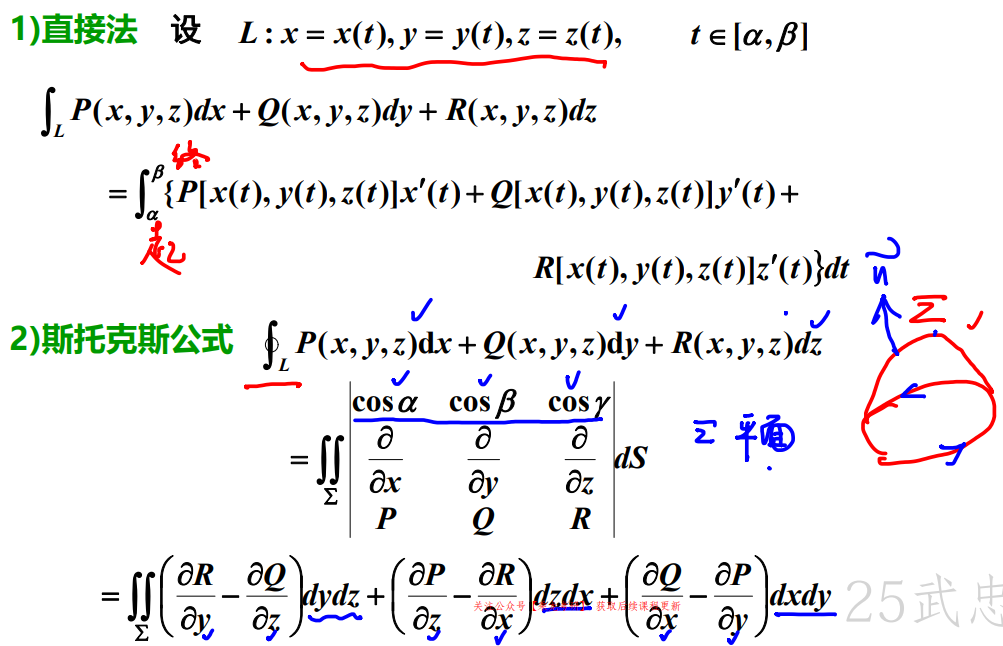
斯托克斯公式将线积分化为面积分。
公式中的第二种形式更常用。
注意:斯托克斯公式中法向量的正向,是平面边界方向使用右手法则得出的。
化空间曲线为平面曲线
即降维。
只适用于空间曲线是由一个曲面和一个平面确定的形式。
例如平面为y + z = 0,将z = -y代入线积分消去z,将空间线积分化为只有x,y变量的在xOy平面上的平面线积分,积分区域为原本积分区域在xOy平面上的投影,如果是闭区域,可以使用格林公式计算。
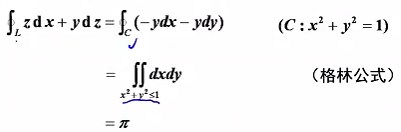
曲面积分
第一类面积分:对面积积分
定义: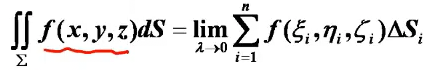
- 其中ΔS_i是积分曲面区域即小曲面块的面积
性质:第一类面积分的值与积分曲面的朝向无关
计算
- 直接求:

其中D是积分曲面Σ在xOy平面上的投影区域。
即把一型面积分化为平面上投影域的二重积分。
注:当给出的形式不能写成z=z(x,y),但可以用其他坐标表示,也可以代入其他坐标求解。
- 利用奇偶性
当曲面关于xOy面对称时,判断函数关于z的奇偶性:
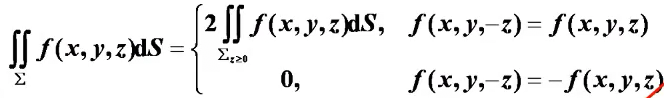
关于其他面对称时类似
- 利用对称性
当积分曲面为球面:x^2 + y^2 + z^2 = 1
此时三个积分变量地位相等,即有变量对称性:f(x,y,z) = f(y,x,z) = f(z,y,x)….
此时可以用:对x^2 + y^2的积分 = 2/3 * 对x^2 + y^2 + z^2的积分
第二类面积分:对坐标积分
定义: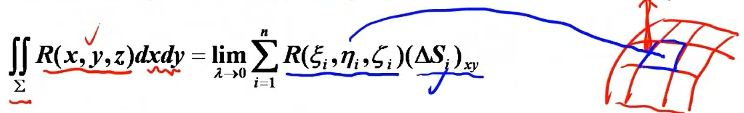
- 此处的积分区域Σ是有向曲面。
- 其中(ΔS)_xy是积分曲面单元在xOy面上的投影:此时有两种,在曲面上侧做为投影面积,在下侧做投影为面积的相反数(都是数)。
性质:改变曲面方向,积分值加负号。(与一型的本质区别)
计算
- 直接求:
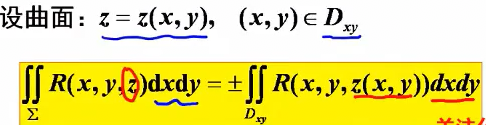
即将面积分化为在xOy面上投影的二重积分。
注意:二型计算时要考虑正负号,在上侧投影为正,在下侧投影为负。
当积分区域为平面(例如x=C或者y=C),此时在对应平面方向上的投影为直线,此时面积为0.
当曲面有其他写法时:
例如x=x(y,z),此时在yOz面上投影,前侧为正,后侧为负。
在计算
Pdydz + Qdzdx + Rdxdy时,如果不能用高斯,可以将微分化为一个平面上的投影:例如化为Dxy,则为:
$$
[P*(-z’_x) + Q*(-z’_y) + R] * dxdy
$$
- 高斯公式
对封闭曲面外侧的面积分 与 封闭曲面对应空间区域的三重积分 建立关系的公式。
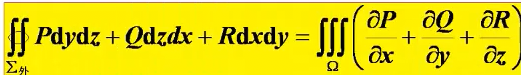
与格林公式类似,如果曲面不封闭,可以补面用高斯公式。
- 使用高斯公式要特别注意曲面的朝向和化为三重积分后的正负。
注意:如果给出的区域为曲面,化为三重积分之后,积分区域是对应的空间体,因此不能将曲面方程直接代入积分式中简化。
实际上:只有线积分和面积分直接求时可以代入,二重和三重积分都不能代入(因为积分区域是范围/区域)
两类面积分的联系
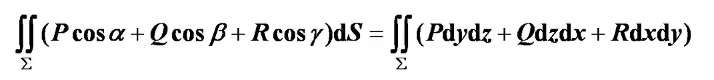
注意:(cosα, cosβ, cosγ)是有向曲面块在该点的法线的方向向量。
多元积分应用
场论初步
方向导数
定义:
$$
\frac{\partial f}{\partial l}\left| \left( x_0,y_0 \right) \right. =\underset{t\rightarrow 0^+}{\lim}\frac{f\left( x_0+t\cos \alpha ,y_0+t\cos \beta \right) -f\left( x_0,y_0 \right)}{t}
$$
计算: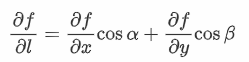
注意:cosα和consβ 为方向余弦 = 方向向量 除以 单位向量(即需要单位化)
若z = f (x, y)可微(可微时沿任何方向的方向导数均存在)
$$
\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}\cos \alpha +\frac{\partial f}{\partial y}\cos \beta
$$
梯度
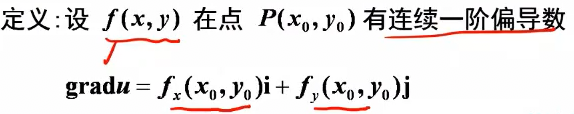
计算公式: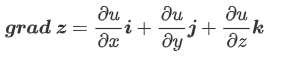
即梯度为函数在某点处,三个坐标的偏导数代入坐标得到的向量。
$$
\boldsymbol{A}=\left{ P,Q,R \right}
$$
$$
\boldsymbol{grad\ z}=\frac{\partial u}{\partial x}\boldsymbol{i}+\frac{\partial u}{\partial y}\boldsymbol{j}+\frac{\partial u}{\partial z}\boldsymbol{k}
$$
梯度是一个向量,代表方向导数最大的方向,梯度的模即为方向向量的最大值。
散度
是一个数: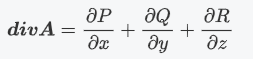
$$
\boldsymbol{divA}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}
$$
旋度
是一个向量: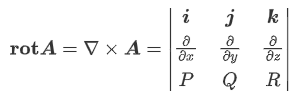
$$
\mathbf{rot}\boldsymbol{A}=\mathbf{\nabla }\times \boldsymbol{A}=\left| \begin{matrix} \boldsymbol{i}& \boldsymbol{j}& \boldsymbol{k}\ \frac{\partial}{\partial x}& \frac{\partial}{\partial y}& \frac{\partial}{\partial z}\ P& Q& R\ \end{matrix} \right|
$$
