暑假日志(八月)

8.1

八月开始，漫无止境的八月~

计网

链路层

结束流量控制和滑动窗口，开始介质访问控制部分。

整体难度一般，需要注意：

• 窗口大小 = 发送窗口 + 接收窗口 <= 2^n（用于帧编码的比特数）

• 发送窗口最大为2^n - 1

  • 即窗口大小为k时，最多有k-1个帧已发送且未确认
  • 如果有k个帧已发送，则对接收方来说，可能出现两种0-k帧：
    • 0-k帧全部到达，并已经被确认
    • 0-k帧全部丢失，此时为重传，全部未被确认
  • 两种可能无法确认，因此最多为k-1大小

• 接收窗口一定小于发送窗口

• 信道利用率：

  • 对停止-等待：T_d / T_d + RTT + T_r

    • d为deliver发送时延，r为receive接收时延（即接收方发送确认帧的传输时延）

  • 对ARQ有两种情况：

    • n*T_d < T_d + RTT + T_r：

      • 利用率 = n*T_d / T_d + RTT + T_r

    • n*T_d >= T_d + RTT + T_r:

      • 利用率为 1（即连续发送）
      • 好吧实际上是一种情况

    • 因此可以推出分组长度越大信道利用率越高，此时计算最少分组数时，需要用最小帧长度计算

线代

行列式每一项的组成：不同行且不同列元素的乘积，再乘逆序数

• t(4321) = 3 + 2 + 1 = 6

• 行列式的项编号位a_ij，其中i为列数，j为行数

概率论

参数估计

这部分难度不大，但概念很多。

参数估计实际上就是用给出的样本数据，估计未知的总体分布参数。

有两种：矩估计与最大似然估计

• 矩估计：直接计算样本的原点矩，几个参数就求几阶，再列方程组求解

  • 注意:如果一阶矩(即样本期望)为0，例如对称区间的均匀分布，此时不能计算，需要用二阶矩做参数估计

• 最大似然估计：将所有样本的分布律或者概率密度函数累乘得到L(x)，取让L最大的x为参数估计

  • 求对数简化计算
  • 求导得(lnL(x))’ = 0求极值
  • 再求二阶导确定极值是极大还是极小/还是非极值（此时需要用单调性或者定义求最大值）

其实也不能，就是算定积分而已。

• 估计值的评估：

  • 无偏性：对估计值代入的分布求期望，如果等于总体均值则为无偏估计，例如E(X-) = u
  • 有效性：D(x)更小的估计值更有效

• 置信区间

  • 对估计值与总体分布的可信度评估
  • 

假设检验

一样是概念很多。

假设检验用于判断一个给出的假设，对当前给出样本对应的总体，是否是合理的。

计组

还是与IEEE-743搞来搞去，这部分题目是真多啊。

• 反直觉：int转float也可能损失精度

• 字节地址编码：地址中一位不是1bit，而是1byte，即一字节。

  这个我一直搞错了////

• 长度对齐：int为4，unsigned = unsigned int也是4，char为1

  • 地址从0开始计算，对齐要求：起始地址 % 数据长度 = 0
  • 注意最后结构体整体长度，要是其中最长数据的整数倍

8.2

线代

伴随矩阵最重要的性质：A^-1 = A* / |A|

可以推出：AA^-1 = AA*/|A| = E

其他判断是否等价的式子大多都可以用两边取行列式判断，大多数都是|A| = 0但不能推出A=0。

• 行列式中有成比例的向量时，行列式为0

概率论

今天终于结束概率论的660填空题和基本复习了。

置信区间

用上面的假设估计给出总体分布的参数估计时，可以用无偏/有效性等性质衡量，但不能量化。

置信区间就是对估计可信程度的量化：

P{ λ(X1,X2...) < λ < λ(X1,X2...) } = 1 - α

其中这个区间λ的取值区间称为置信区间，α称为置信度。

实际上计算时，通常是将给出的估计值代入总体分布，再化简到只有参数的形式，用具体分布的上分位数计算

假设检验

这部分是对置信区间理论的延申。

当给出的不是确定的估计值，而是某种论断时，如何根据样本判断这种对总体的论断是否可靠。

需要用拒绝域的概念，即将给出的论断称为H0，其对立的论断为H1.

此时有两种错误应该避免：

• 第一类错误：H0为真，且落入拒绝域内被拒绝
• 第二类错误：H0为假，且未落入拒绝域被接收

对第一类错误尽量减少的推断称为显著性检验。

实际上就是将H0成立，然后代入：

P{|X - u| <= k} = α

那么如何确定k呢？实际上知道X的分布，已经由α确定，即z_α/2，X的上分位数。

化简即可求出拒绝域。

注意置信区间与拒绝域显著性水平写法不同，一个是1-α，一个是α

计网

结束介质访问控制(MAC)层。

这部分内容很多，而且有点复杂，但搞明白就不难。

另外408的计网在这部分的考察明显比本科课程要难，除了以太网的CSMA/CD协议，还对无线网802.11协议的CSMA/CA有不低的要求，王道书上写得不多，要看谢书才能理解。

• 争用期和最小帧是CSMA/CD协议的核心

  • 争用期：有两种写法：

    • 2t，即传播时延的两倍
    • 发送最下帧长的传输时延

  • 最小帧长度：与争用期紧密联系

    • 以太网中规定最下帧长度为64字节，即512bit

    • 此时争用期与以太网传输速率有关

      • 对10Base-T（即10Mb/s）：

      • ```latex
        2t = (64*8/10^(7)) = 51.2us

        - 100Mb/s：
        
        - ```latex
        	2t = (64*8/10^(8)) = 5.12us

计组

终于搞定了第二章，老实说比想象的难太多。

尤其是浮点数部分，但好在搞明白之后，做题正确率还是很高的。

• 浮点数表示范围：
  • 最大正数：
    • 最大阶码：阶码不能全1，因此最大值为1111 1110，因为是移码，即254-127 = 127
    • 最大尾数：尾数可以全1，1.1111…1 = 2 - 0.0000….1 = 2 - 2^-23
    • 2^127 * (2 - 2^-23) = 2^128 - 2^104

其他特殊值：

1. 零。若 指数 为 0，小数部分 也为 0，则该数为 ±0。
2. 无穷。若 指数 为 2^e-1，小数部分 为 0，则该数为 ±∞。
3. 非数。若 指数 为 2^e-1，小数部分 非 0，则该数为 NaN。

形式	指数	小数
零	0	0
非规约形式	0	大于 0 小于 1
规约形式	1 到 2^e-2	大于等于 1 小于 2
无穷	2^e-1	0
NaN	2^e-1	非 0

可以看到除了 NaN，从上至下，数值的 绝对值 和对应 指数 都是越来越大的。下面以 32 位单精度浮点数 符号位（ 1 位）+ 指数域（ 8 位）+ 尾数域（ 23 位） 为例，直观介绍其在计算机中的存储。下表中，最大最小均指 绝对值，符号位的 * 表示 可正可负，正为 0，负为 1。

类别	符号位	实际指数	偏移指数	指数域	尾数域	数值
1	*	0	127	低 7 位为 1	全 0	±1.0
零	*	-127（保留）	0	全 0	全 0	±0.0
最小非规约数	*	-126	0（偏 126）	全 0	最低位为 1	±2^(-126)*2^(-23)
最大非规约数	*	-126	0（偏 126）	全 0	全 1	±2^(-126)*(1-2^(-23))
最小规约数	*	-126	1	最低位为 1	全 0	±2^(-126)
最大规约数	*	127	254	高 7 位为 1	全 1	±2^127*(2-2^(-23))
无穷	*	128（保留）	255	全 1	全 0	±∞
NaN	*	128（保留）	255	全 1	非全 0	非数

着重关注以下 4 点：

1. 实际指数的 -127 和 128 保留，分别表示 0 和 ∞/NaN。
2. 规约数指数偏移量为 127，非规约减 1。
3. 最大非规约数尾数域 + 最小非规约数尾数域 = 1
4. 最大规约数尾数域 + 最小非规约数尾数域 = 2

浮点数加减

五个过程：对阶、尾数求和、规格化、舍入和溢出判断

具体细节参见这篇很赞的博客。

8.3

今天下暴雨，晚上就摸鱼了。

线代

关于矩阵秩的部分性质很多，今天才搞明白。

• 对m*n的非方阵A，0 <= r(A) <= Min{m, n}

  • 即mn中较小的值，是矩阵秩的最大值

• 若有AB=0，r(A) + r(B) <= n

  • 其中n为A的列数/B的行数
  • 这个性质可以从矩阵方程的解推出，即写成Ax=0，其中：
    • 解向量个数s = 未知数个数/A列数n - r(A)

• r(AB) <= Min{r(A), r(B)}

  • 在A/B可逆，或者其中一个矩阵满秩时取等号

• r(A +/- B) <= r(A) + r(B)

• 伴随矩阵A*:

  • n r(A) = n
  • 1 r(A) = n-1
  • 0 r(A) < n-1

概率论

又复习了下置信区间和检验估计，至少概率论有线代的掌握水平了。

高数

级数

这部分有点难度的，但基本概念要搞明白：

• 收敛级数 + 收敛 = 收敛

  • 收敛 + 发散 = 发散
  • 发散 + 发散 = 不确定

• 对收敛级数，随便加括号，级数仍然收敛

  • 但如果加括号后的级数收敛，原级数不一定收敛
  • 例如1-1+1-1+1…
    • 加括号时收敛于0
    • 不加括号时一直在-1和+1震荡，没有极限，是发散的

• 对交错级数的敛散判断：

  • 对S_2n求n趋近于无穷，如果于S_2n-1相等，则级数收敛

主要是非常灵活，所以要仔细研究下才行，至少现在是没有能直接轻松做660的余裕的。

8.4

线代

向量组线性相关的题目，两种思路：

• 化为向量组/矩阵的秩
• 直接用定义硬算判断能不能用其他向量表示

高数

级数

依旧是级数部分，把幂级数部分复习完了，但题目还是不太会做。

• 阿贝尔定律：幂级数某个点x_0收敛，则x<|x_0|时，级数绝对收敛
  • 推论：某个点x_0处级数为条件收敛时，幂级数的收敛半径为x_0
• 换元要注意哪个是目标哪个是条件，另外a_n确定时，x^n或者(x-1)^n的收敛半径都相同
  • 但收敛区间/收敛域不同

概率论

这部分有点难度的，还是基础概念的问题：

• 不可能事件(事件为空)与概率为0

  • 不可能事件一定概率为0，但概率为0不一定是不可能事件
    • 即概率为0的事件不是不可能发生，例如平面上某点的概率是0，但一定是可以取到的。
  • 大部分情况只能推出概率，不难得出事件是否是不可能

• 差事件：P(A-B) = P(A) - P(AB)

  • 注意：含义是A发生的同时B不发生，是两个事件的积而不是和

• 互斥/互不相容事件：

  • 即A发生的同时B一定不发生，或者B发生的同时A一定不发生
  • 但A不发生，不一定B发生，即还要A、B都不发生的情况存在

计网

链路层

MAC帧的问题难度不大。

8.5

线代

依然是大部分虐菜，但对线性相关的概念仍然有新理解：

• n个线性无关的向量，最多能表示n个线性无关的向量

• n个向量线性无关，则其任何子向量都线性无关

  • 但若线性相关，则可能有向量是彼此线性无关的

• 已知矩阵的最简型，求一个极大无关组时，注意结果是不唯一的

  • 除了常用的台脚对应的列向量是极大无关组以外，判断是否是无关可以将对应的向量组成“子式”判断是否结果为0，不为0时该矩阵子式对应的列向量线性无关

概率论

整体难度不大，但要注意：

• 给出条件为概率时，不能推出事件的结论

• 有关与级数相关的计算：泊松分布的分布律为k^λ * e^-λ / k!，求其和1，则可以推出：

  • $$
    \sum_{k=0}^{\infty}{\frac{x^k}{k !}} = e^k
    $$

  • 

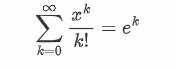
k写成x就是常用的e^x的泰勒展开式。

高数

今天大部分时间都花在级数上了，但好在是值得的，把大部分概念和题型搞明白了。

• 求幂级数的收敛半径一般不难，就两种方法：直接比值求极限和开n次方

• 但求得收敛区间之后，如何判断端点是否收敛/求收敛域就很麻烦了

  • 大部分需要用比较申敛，与p级数比较，或者直接求导判断单调性

    • 注意：判断单调性时，例如莱布尼茨定理用第一条要求判断递减，只需要n > N时递减即可

    • 因为级数删去有限项，不影响整体收敛半径和敛散性

  • 对负数形式，大部分要拆成(-1)^n形式判断交错级数收敛

• 求幂级数的和函数

  • 这个是难点，关键是要完全记住五个常用的麦克劳林公式，然后把给出形式转化为基本公式的函数即可

  • 凑交错级数：x^n = (-1) * (-1)^(n-1) * (-x)^n

    • 实际上是用(-x)^n凑出来(-1)^(2n-1)。

    • 注意只能是x^n类型才可以凑，如果是2n-1这种必然是奇/偶时不可能凑出来

    • 这个最常用用于凑ln(x+1)的形式

      • 注意：ln(x+1)的展开式形式有一点特殊：求和是从1开始而不是从0

• 换元时要注意：

  • 最好凑乘法换元，而不是用加法
    • 例如1/(x+1)，凑1/(ax + 1)而不是1/[(x+a) + 1]

8.6

线代

惯例先做线代，有复习了个有用的知识点：

• 线性方程组的基础解系，是解集的极大无关组
• 非齐次线性方程组的一大堆特解，线性组合之后仍然是解的充要条件：
  • 所有参数之和为1
  • 线性组合之后是对应导出组特解的条件：所有参数之和为0

高数

终于搞定了级数这部分，确实不简单。

关于幂函数，主要就两种：

1. 求级数的和函数
2. 求函数的展开式（麦克劳林或者泰勒）

彼此相反，多数用到两种思路：

• 直接凑常用的五种麦克劳林

• 用逐项求导和求积分级数不变

  • 还有一种，即可以求出S(x)的导数与函数本身的关系，此时可以用微分方程求解

    注意：实际上是用级数由无限性决定性质，所以有限项可以构造和凑

注意：这两种题目都要写收敛域，五种常用麦克劳林中，需要特别注意ln(x+1)是(-1,1]，1/(x+1)是(-1,1)

换元时，收敛域要改变：例如x^2代入ln(x+1)，此时收敛域变为[-1,1]

概率论

难度不大，但错了不少。

分布函数的性质和要求：

1. 右连续
   • 这个很重要，实际上是因为定义中P{X<=x}，即包含了X=x的概率，所以需要用右连续F(x) = F(x+0)
2. 单调不减(即要么是常函数，要么递增)
3. 趋近于负无穷时为0，趋近于正无穷时为1

概率密度的要求：

• 在R上就定积分为1

计网

网络层

注意，判断某个地址是主机还是广播时，先看第一个地址位，判断是A/B/C，再找主机号，不能直接看最后一位

8.7

计网

网络层

继续做题，这部分题目是真多啊。

线代

特征值和特征向量部分，意外的有点难度：

• 特征值/特征向量定义的两种用法：

  • Aα = λα
  • |A-λE| = 0

• A的特征值为λ时，A的函数f(A)的特征值为f(λ)

  • 例如A^2的特征值为λ^2，且特征向量相同

  • 但注意，此性质不能反推，即如果有A^2的特征值为λ^2，不能推出A的特征值为λ

• 判断两个矩阵相似：

  1. 证明两个矩阵都可对角化
     • 两种方法：1. 矩阵的特征值均不相同 2. 最大特征值重数 = n - r(A - λE)
  2. 特征值完全相同

• 如何通过给出特征向量和特征值构造可逆矩阵P判断相似：

  • 当有P^-1 * A * P = B 或者 AP = PB时，如果B是对角矩阵：
  • 此时P由特征向量组成，B由特征值组成，且特征向量的k倍仍然是特征向量
  • 此时只需要特征向量与特征值是对应即可————例如特征值2对应α，在P和B的位置是相同的

概率论

只有一个地方要注意：

• P{X>x, Y>y}不是1 - F(x,y)
• 而是1 - F_X(x) - F_Y(y) + F(x,y)，画图就很容易看出来了，另外要记住边缘分布的定义
• F_X(x) = F(x, +∞)

高数

向量代数和空间几何，主要是三部分：

1. 确定平面方程：

   • 常用：一个点，两个不平行的向量，此时可以用混合积确定一个平面

     • 实际上就是三个点共面，列个行列式为0的方程解出来即可

   • 找一个点和法向量

2. 确定直线方程：

   • 点 + 方向向量可以写对称式或者参数式
   • 常用：两个不平行平面的交线，此时问题就转化为了求平面方程

3. 直线在平面上投影：

   • 一般是用两个平面的交线，即关键在如何解出一个垂直的平面
   • 如果给出了直线，但未直接给出点，可以带个x=0或者y=0构造一个已知的点。

8.8

线代

复习二次型，主要是配方法。

2015年数一真题

做了一套15年的，整体难度不大，但做题效率不高。

周末可以安心去看live了:)

计网

IPv6：

• 禁止路由器分片，只能端到端分片
  • 路由器遇到过长的报文直接丢弃
• 报文首部固定长度，且与IPv4相比删去了首部校验和字段
  • 因为物理层和链路层已经对此有校验了。

8.9

明天去少女乐队only咯~

今天下暴雨，效率一般

线代

终于搞定了660的全部线代部分。

今天做完了二次型的选择题，复习的合同、正定等概念就懒得写了。

主要搞明白的是之前没搞懂的二次型标准化的“配方法纠结如何配方”：

• 对x1，先把包含x1的所有项写在一起，然后凑成平方项的形式

  • 注意：当包含类似于x1x2-x1x3这种多个项的形式时，可以看作一项：x1(x2-x3)再配方即可

  • 参数也有加进去配方，关键是一定要把x1结束在这一步，否则后面配不出来

• 再对其他项做这个操作

还有一个地方：可以写成标准型的形式，不一定是标准型，因为可能变换是不可逆的

概率论

有个之前没搞明白的：

• 二维随机变量与一维随机变量函数是不同的，即(X,Y)与Z=XY是不同的。

  • 好吧这个应该是常识。

• 二维变量的条件概率密度，如果XY是独立的：F_X|Y = F_X, F_Y|X = F_Y

• 边缘概率密度：X的边缘概率，是对f(x,y)求在R上对y的定积分

  • 注意：由联合分布可以确定边缘分布，但不能反之
  • 因为不知道边缘分布之间的关系

• 独立性要用好，例如求P{XY-Y<0}，如果X,Y独立，则有：

  • P{XY-Y < 0} = P{Y(X-1)<0} = P{Y>0, X-1<0} + P{Y<0, X-1>0} = P{Y>0}*P{X<1}….

高数

方向导数求法：

1. 求梯度和对应直线的方向向量
2. 方向导数 = 梯度 * 方向向量/向量的模

另外依然是空间解析几何：

• 求绕轴旋转的曲线表达式，关键是找到旋转中的不变量————即原本的点与旋转之后点的关系
• 大多数是用到轴的距离不变来求的

如果给出是对称式，可以改写成一般表达式或者参数方程再代入关系式

计网

路由选择算法，整体难度一般。

唯一需要搞明白的是，RIP坏消息传播慢的原理：

• R1发现一个链路N不可达时，在路由表写为16，但此时收到R2的路由信息，是R1原本距离+1
• 此时R1误以为N又可达了，因此更新路由表为R2路由距离值 + 1
• 之前R2再更新，循环直到16。

8.10

少女乐队only

第一次去livehouse看了乐队的live，很有趣。听了kon的歌和God knows，真的很棒。

Louder和猛独也是超爽。

想要下次搞个应援棒来了。

大概我人生中又有许多钱是精力会花在这上面了。

但确实是很迷人、很美好的事。

爱与勇气传达给你。

8.11

昨天打call太累了，今天比较摸鱼。

计组

终于把卡了好久的主存储器部分搞定，很有难度，看了好几遍才搞明白。

• SRAM与DRAM的区别：

  • 大部分很直观，最关键的部分是DRAM为了减少地址线数目，使用引脚复用：
  • 即将行地址和列地址分两次输入，因此只需要一半的引脚数

• 按字节编址和按字编址：

  • 分别是指两种存储单元所对应的信息个数。
  • 按字节是一个存储单元包含一个字节，即八个比特
  • 按字与CPU字长有关，如果字长为4B，则一个存储单元（即地址的一位）包含四个字节

• 交叉寻址：

  • 如果是轮流启动各个存储块，块数 = 存取周期 / 总线周期
  • 总线周期：CPU通过总线对存储器请求的周期

• 多个DRAM扩展时：

  • 这部分和之前学的区别不大，但要注意：

  • 给出的是地址时，要注意片内用到了几位，再对剩下的尾数做片选

8.12

概率论

二维随机变量分布函数的要求：

其他与一维没区别，唯一多的是这个：

• 落在矩形区域内的概率非负
  • 因此当只有一半平面例如y>x这种不能满足分布函数的要求

高数

三重积分：

• 先一后二/先二后一

  • 这个看起来很容易，但用起来其实有点难度

  • 先一时先对z求定积分，此时上下界为积分区域的上下曲面用z表示

    • 做一条平行z轴的直线，射入点位为上界，射出为下界
    • 然后再对D_xy上的投影做二重积分

  • 先二时先求积分区域截面D(z)的二重积分，再求整体对z的定积分

    • 如何求截面D(z)？

      • 做积分区域在另外两个平面的投影，用z表示x和y即可

    • 此时定积分上下界为z(值)的范围

• 记忆起来：实际上是信息量的分配不同

  • 先一是把信息量分配在对z的定积分，投影好求
  • 先二是把信息量分配在截面的二重积分，难点是求截面

• 因此，如果投影容易求，此时用先一更好

• 或者给出的被积函数很容易（例如只有一个变量），此时求截面后可以只用面积而不用求积分，此时用先二更好。

8.13

概率论

求与变量的数字特征相关的数学关系：

• 直接求定积分/换元
• 凑数学期望或者方差的表达式再代回

对不能直接看出来的分布，可以列几个看看

• 尤其注意有X=0的分布，可以导致期望可以很容易求出来

高数

依然是三重积分/线面积分

球坐标：

• 积分区域是球或者圆锥体时，一定要考虑下球坐标

• 三个变量：平面角，与z轴正方向夹角，距离

  • 注意：这里的距离和z轴夹角，都是相对于原点而不是圆心

• 其实z轴夹角最不直观，需要思考下，例如球心在原点时，夹角范围为[0,pi]

轮转对称性：

• 这个最常用，但不容易想到

• 尤其在三重，主要是两种：x+y+z=1 或者 x^2 + y^2 + z^2 <= 1

  1. x^2 + 2*y^2 + 3*z^2 = 6z^2
  • 注意：这里求三重积分时，可以换为可以方便求的变量
  • 例如求xOy平面的截面比较容易，则换位对6*z^2求三重积分
    • 此时无需求积分，求出截面面积即可
  2. 反用：给出为x^2时：
     • 凑为1/3(x^2 + y^2 + z^2)
     • 如果是求面积分，此时可以化为半径平方，此时求球体表面积即可（这个离谱了）

质心/形心应用：

• 如果给出有形如对单个变量的一次方，例如对x求球体的三重积分
• 此时可以化为:球体的形心x坐标 * 球体面积
  • 即逆用形心计算公式，此时形心坐标为球心

计网

TCP

难度一般，但题目不太好做。

• 注意拥塞窗口的单位是MSS，因此如果MSS=2KB，则起始大小为2KB
• TCP建立连接，对一方：只会占用一个报文段序号

8.14

概率论

660概率也结束了。

两个要点：

• 样本均值与样本方差独立
• 样本均值与方差的分布：
  • 均值满足正态分布：参数为u和σ^2/n
  • 方差满足卡方分布：(n-1)S^2 / σ^2 ~ X^2(n-1) 满足参数为n-1的卡方分布
    • 注意：将S^2中的均值换为总体期望时，满足自由度为n的卡方分布

另外卡方分布的两个特征：

1. 期望为n
2. 方差为2n

高数

线面积分

这部分难度无上限啊，各种对称性。

主要有两个地方仔细思考了：

1. 求第二类面积分时（第一类就直接代入sqrt(1+z_x’^2+y_x’^2)就完了），要注意投影方向：

   • 计算时，将别积分曲面投影到平面上，例如投影到xOy，求出投影区域Dxy作为二重积分区域，然后将被积函数中的z用x和y表示
   • 注意：当给出为f(x,y,z) dxdz的形式，如果要投影在xOy上，需要将dz化为dy：
     • 即dz = - z_y' * dy，要注意这里对y求偏导时要加一个负号
     • 这个负号是隐函数推导时加的
     • 另外要注意这个负号与投影方向加的正负号不可混淆

2. 椭圆极坐标换元

• 这部分甚至牵扯到换元的基本原理，即换元之后参数的计算：雅可比行列式

• 单纯计算的话，记住这个换元：

  • x = r * a * cos(t)
  • y = r * b * sin(t)
  • 容易看出，这种换元仍然保持了与圆的极坐标类似的：x^2 + y^2 = r^2

• 换元之后如何代入二重积分呢？

  • 对t做积分，再对r做[0,1]的积分（这部分对椭圆是固定的）
  • 最后乘abr即得到结果

给出一个完整例子：

计网

TCP计算没什么难度，但很容易错。

• 例如计算发送了多少字节数据，要注意序号是第一个字节，例如1000，如果长度为400B，则发送的最后一个字节序号为1000+400-1=1399，此时返回确认的ack值为1400.

• 动态滑动窗口：

  • 如果发送了400B，起始字节序号为500，结果接收到ack=500的确认报文，此时说明：

  • 前面发送的500报文段还没有收到，此时的确认是对之前报文段的

  • 因此如果确认报文的rwnd=500，但之前发送的400B仍然没确认，此时只能再发送100B

8.15

今天效率一般，660几乎没进度（只剩几十道题了）

高数

如果一个区域上下曲面都可以表示为z=f(x,y)的函数，且中间为柱面，则为“长条柱形区域”，其体积：

1. 直接求z_1(x,y)和z_2(x,y)对z的定积分
2. 三重积分，先二后一
3. 旋转体体积公式，转为曲线/直线绕z轴旋转
   1. 绕x轴：pi * y^2求定积分
   2. 绕y轴：2 * pi * x * y求定积分

• 求积分技巧：

  • 遇到0到2pi的积分上下限，且被积函数为三角函数的偶次方时，可直接化为4 * [0, pi/2]

计组

cache部分，这部分很难，三十多题错了八道。

• cache与CPU按字为单位交互，cache与主存以块交互

  • 当cache没有命中时，会从内存将整块数据加载到cache。

• cache的块大小与主存块大小相同

• 命中率与块大小没有直接关系，但cache越大命中率越大

• 标志位中的替换控制位与脏位 和 具体替换策略与写入cache时的回写/直写有关。

8.16

高数

660三重积分和线面积分的填空做完了。

顺便也看完了全书多重积分的几何应用和物理应用。

几何应用感觉很有意思：

• 空间平面的面积与其投影在坐标平面上面积D_xy的比值：

  • σ = D_xy / |cosγ|
  • 其中γ为平面法向量与z轴正方向的夹角
  • 即cosγ为法向量的方向向量

• 这个结论很好用，但注意不能直接用在斯托克斯公式上。

  • 因为斯托克斯公式计算的是空间曲线的第二类线积分，化为二重积分之后，积分单元为dxdy或者dydz/dzdx，但空间平面的面积要求积分单元是dS

  • 对斯托克斯公式结果的化简：对空间平面在dxdy上求面积分 = 对该平面在xOy面上的投影求二重积分

• 对曲面z=f(x,y)截取柱面时，截面的面积计算：对f(x,y)在xOy的投影求二重积分

• 补线用格林或者高斯时，一定要记住注意方向

  同时也要注意面的朝向或者线的方向：

  1. 正向：区域在左边
  2. 负向：沿方向区域在右边

计组

虚拟内存与cache

• cache的标记项中，如果是直接映射/分组映射，不包含行号/组号

  • 因为标记项中用基于内容查找，但行号是基于索引查找
  • 因此没有必要包含，只需要标记位Tag即可

• TLB的页表的缓存，查TLB不需要与主存交互

• 段页式存储仍然是基于“页”的，其中的段只是逻辑结构

计网

DNS + FTP + 邮件协议

没什么难度。

• 邮件发送协议：SMTP
• 邮件接收协议：POP3

DNS的两种查法：

• 迭代：发多个请求
• 递归：发一个请求，直接从最近的本地DNS服务器获取响应

注意：第三级的权威服务器可以有多个，取决于子域名个数

8.17

高数

重积分物理应用 + 级数选择题

难度不大，级数选择题出乎意料的全对了：

• 几个主要参数：

  • 梯度grad：向量(f_x’, f_y’, f_z’)
  • 旋度：向量
  • 转动惯量div：数

• 级数的命题判断难度不大，主要是线性关系和基本性质

计组

指令系统

难度一般，但与前面的数据部分结合起来有难度。

• 最低有效数据：即最低位数据
• 大端小端
• 变址寻址的变址寄存器IX，如果是任意时，在地址中也要写明（即寄存器号要占几位）

8.18

下午去天府红摸鱼了。

不知道为什么这回对地偶兴趣不高，明明也看到了之前的几个。

另外想了想感觉谷子盲盒这玩意其实是很聪明的设计：

偶像化的任何企划（动画也好漫画也好游戏也好），如果要出单人的周边。

就必然面临不同角色人气不同的难题，该如何定价？如何生产？很麻烦。

盲盒就搞定了这个问题：相对于用市场/调价做了一次动态调整。

高数

级数选择题，难度还好

• 主要是正项级数申敛法的本质：前n项和有界

  • 推论：正项级数an收敛，则a_2n-1和a_2n均收敛

• 级数a_n收敛，但a_n^2不一定收敛

  • 正项一定收敛，但交错不一定
  • 例如(-1)^n * 1/sqrt(n) [这个反例应该记住]

• 级数收敛 => 在n趋近于无穷大时，a_n有界 => 存在M，使|a_n| < M

  • 这个结论可用于证明绝对收敛

计组

汇编基础，大部分都学过。

• 补码相减：化为相加，即被减数 + 减数的取反 + 1
  • 此时无需考虑负号或者真值
• OF与CF：有符号溢出位OF，无符号数位CF，但实际上机器数中不区分有无负号，因此对有符号数也可以CF=1，但此时没有含义
• 基于堆栈调用子过程调用，过程要思考下才能搞明白

8.19

高数

660级数选择题

难度不小，主要是放缩最麻烦：

• 当已知a_n的收敛半径R时，推不出n趋近于无穷时，|a_n+1 / a_n| = 1/R

  • 因为极限不一定存在
  • 此时要推导a_n的函数的级数收敛半径，应该用逐项求导/求积分收敛半径不变

• 当给出是具体x值的级数时，求和可以用两种方法：

  • 先求前n项和S_n，再求n趋近于无穷时的极限

    • 比较有技巧，例如n*q^n型可以拆开，一项是等比，再将其中一项凑为S_n

  • 化为函数项级数/幂级数求和即x^n

    • 一般会用求导/求积分，注意(-1)的幂次，这里很容易错

    • 可以用S(x)化简给出的级数

• 放缩：

  • (注意只需要在n大于N时，满足大于关系即可，不需要每一项都满足)

  • lnx < x

  • (lnx)^2 < x

计组

中央处理器

终于到重头戏了，计算机就是搓碟，CPU的核心就是四个周期。

搞明白，真能手搓CPU哇。

• 指令流程：

  • 取指周期
  • 间址周期（对间接寻址的指令）
  • 执行周期
  • 中断周期

• 各个阶段的对应指令也不太难

• CPU取指令只能从PC中，因为即使有跳转，也是先更新PC的值

• 各个周期称为“机器周期”，因为各个传送阶段只需要几个时钟周期（节拍），影响很小，所以可以将机器周期简化为存取周期（访存涉及的时间最长）

  • 推论：当存储字长与指令字长相等时，一次访存即可取出一条指令

    此时取址周期 = 机器周期 = 存取周期

  • 为方便取，指令字长应该为存储字长的整数倍

8.20

高数

立体解析几何/三重积分

• 确定一个平面：平面上一个点的坐标 + 法向量

  • Ax + By + Cz + D = 0中(A,B,C)为法向量

• 低级错误：已知直线的对称式，转为一般式时，注意是A(x - x_0)而不是Ax

• 对称性应用：判断函数对某个变量的奇偶性：

  • 例如已知积分区域为上半球面，则相对于xOz和yOz平面对称，此时对x和y为奇函数时为0，为偶函数是倍数
  • 对偶函数:此时可用f(x,y,z) = f(-x,-y,z)判断，因此zdV可以偶函数对称性

2003年数一真题

感觉比15年难不少，而且十道大题体量太多了。。。

• 多重微分极值判断：

  • AC-B^2 > 0时极值存在：

    • 判断极大/极小：
    • A>0极小
    • A<0极大

  • AC-B^2 < 0时极值不存在

    注意不要与上面的极大/极小判断搞混，AC-B^2<0就一票否决了

• 傅里叶展开

  • 对周期为2l的连续函数：f(x) = a_n/2 + ….(后面忘了>_<)
  • (-l,l)上偶函数/偶拓沿：
    • f(x) = 1/L * Σa_n cos(n * pi * x / L)
    • a_n = 2/L * 对f(x) * cos(n * pi * x / L)在(0, L)上求积分
    • 注意偶函数的傅里叶参数a_n与周期函数不同
    • 尤其注意前面的系数是2/L和积分区间在(0,L)而不是(-l,l)

• 线代部分：

  • 两个方程组Ax=0与Bx=0同解，与对应系数矩阵的秩相同的关系：

    • 同解 => 秩相同

      反之不成立

    • 推论：当A的解同时也是B的解时，有r(B) >= r(A)，反之不能由秩的关系推出解的关系

  • A与A*的特征值与特征向量关系：

    • 若A的特征值为λ，则A*的特征值为|A|/λ

      可以由此推出A^-1的特征值为1/λ

    • 特征向量：若A的特征向量为α，则A*的为P^-1 * α（这个很容易忘记！）

8.21

高数

660三重积分/线面积分选择题

660倒计时了。

整体难度不大：

• 格林公式转化为二重积分后如何确定正负号：

  • 二类线积分的方向为正向：即沿曲线方向，二重积分区域在左侧
  • 此时为正，反之为负

• 一类线/面积分与二类线面积分的转化：

  • (Pcosα + Qcosβ) ds = Pdx + Qdy

    其中的α和β为曲线“切向量”的方向余弦

  • 可由法向量转化为切向量：cos(α_法) = cos(β_切)

• 对向量求偏微分：

  • 例如u=f(x,y)对法向量n=(x,y)求偏微分
  • 此时实际上为u_x' * cosα_法 + u_y' * cosβ_法
  • 注意这里的余弦值为法向量

概率论

置信区间：

• 搞明白关键定义：对参数的区间估计

• 例如对u的估计，用样本均值X_表示，要确定在某个可信的范围内，此时有定义：

• P{|u - X_ < k |} = 1 - α

• 此时k被1-α确定，为z_α/2

  • 因此问题就转化为对样本均值X_的分布求解再化简了
  • 注意这里只能有一个参数未知，否则无法化简（即枢轴量的概念）

• 详细推导参见这篇博客，写得很清楚。

求样本函数分布：

• 若用样本函数α = min{X1,X2….XN}估计某个参数，需要求α的分布
• 此时可以直接用随机变量函数的分布做，也可以用F(x) = P{X<=x}推导
  • 因为独立，所以有：F_min(x) = 1 - [1 - F(x)]^n
  • max函数时为：F_max(x) = F(x)^n

8.22

高数

The end of 660

660结束，今天的题目全对了。

• 方向导数是“数”，梯度是向量

  • 最大方向导数是梯度的模

• 方向导数求法：先求梯度，再用梯度点乘方向向量的方向余弦

  • 这些都是之前就知道的，但有个有意思的地方：线面积分的一类与二类转换可以与方向向量联系起来

  • 即实际上一类转二类就是乘的曲线/曲面切线的方向导数

    因此可以用在斯托克斯公式转化为第二类面积分之后

• 曲线切线的一种求法：

  • 如果给出曲线是曲面与平面的交线，则曲线切线一定满足：
    • 与曲面法向量垂直
    • 与平面法向量垂直
  • 此时可以用n1 X n2 = 切线方向向量
  • 注意这里是叉乘

计组

指令流水线

几乎是最后一个有难度的内容。

• 为解决数据竞争的转发/旁路技术：
  • 注意有旁路时是上一个指令的EX后直接传送到下一个EX，即ALU中，因此跳过了第二个指令的ID取数阶段
  • 因此两个指令可以不阻塞直接流水
  • 但对load-use型的数据冲突不行，因为一定要执行完MEM阶段才能执行下一指令。

8.23

今天没有高数

2015英语一真题

难度真题一般，但错误不少：7完型/5阅读/2七选五

七选五不该错，因为着急吃饭有点草率。

但确实有点难度。

bound熟词生义：除了边界和必然发生，还有开始/出发去的意思

conduct on：固定搭配，意思是研究某种事物

• distort：扭曲
• retort：反驳

计组

总线

控制总线：单向传输，由CPU传输到各个部件时钟周期和控制信号

• 但注意：控制总线上也会传输内存/IO设备等的响应控制信号，但实际上是CPU对外设的中断响应
• 因此方向仍然是单向，即CPU到外设
• 同理：状态总线传输方向也是单向，但是外设到CPU

8.24

高数

880开始

难度还好，不太好做，但正确率挺高。

• tanx的泰勒展开：x + 1/3 * x^2 + 2/15 * x^3 + ...

• arctanx的泰勒：x - 1/3 * x^3 + 1/5 * x^5 - ...

这两个偶尔会用到，尤其是tanx的，很难记住

求极限的思路：当加减项不好求时，可以用提公因式转化为乘除：

• tanx - sinx = sinx (1/cosx - 1)

计组

最后的计组了，居然有点难度：

• 两种中断优先级：
  • 响应优先级：设定为硬件电路的CPU对中断开始执行的优先级
  • 处理优先级：经过屏蔽字修改，即可以被抢占中断的优先级，CPU实际执行完中断处理的优先级

8.25

高数

880继续极限部分，难度还好

• 数列和极限的两种思路：

  • 夹逼定理

  • 提取1/n作为dx，然后化为i/n的函数，求0到1的定积分即可

    • 有时会两个一起用，即先夹逼出范围，再对两个范围用定积分求值

    • 例如分子分母都有变数i，此时可以只确定其中一个做夹逼

      再对另一个i做定积分定义计算

• 求极限时要注意何时可以代入，一般代入后不为0都可以

计组

王道书一遍结束。

• 两种中断：

  • 内中断：即异常，与指令执行有关的中断

    • 例如缺页中断，除零异常等

    • 另外cache缺失不是中断，而是完全由硬件实现

  • 外部中断：与当前指令执行无关，由外部触发的中断

    • 例如键盘/鼠标输入

• 中断周期的两个主要过程：

  1. 中断隐指令：纯硬件完成
     • 关中断
     • 保存断点（即PC寄存器的值）
     • 查中断向量表形成中断处理程序入口地址
  2. 中断处理程序：操作系统内核层程序实现
     • 保存通用寄存器/保存现场信息
     • 执行对应的中断响应程序
     • 恢复寄存器现场
     • 开中断（即关和开分别由硬件和软件完成）
     • 中断处理程序返回

注意这里是单重中断，多重还要再开+关一次中断

• DMA流程：

  • CPU/对应设备驱动程序做预处理
  • DMA数据传输（纯硬件实现）
  • 发送传输结束中断给CPU

• 注意：DMAC的数据缓存寄存器很重要，当该寄存器长度的数据被外设准备好时，设备向DMAC发送DMA请求，DMAC向CPU发送总线请求，此时CPU必须要对该中断做出响应。