古典密码学
经典加密技术
- 代换:
- 明文内容的表示形式改变,内容元素之间相对位置不变
- 明文字母用密文中对应字母代替
- 置换:
- 明文内容元素的相对位置改变,内容的表示形式不变
- 乘积:
- 多个加密技术的叠加
算术密码
- 仿射密码
- 希尔密码
代换密码
单表替代:
- 凯撒密码
- playfair密码(二维单表替代)
多表替代:
- 维吉尼亚密码
这两种密码均无法抵抗频率分析攻击。
课后题:
某加密系统,明文/密文字符集都是英文字母集合。加密算法首先对明文进行单表代换操作,再对代换结果进行置乱操作。该系统是不能抵抗选择明文攻击的。即,攻击者可以设计若干个明文,并得到它们对应的密文,根据这些明文-密文对来破译密钥。问,若每个明文/密文的长度限制为15个字符,最少需要多少个选择明文就能保证破译?
3个选择明文串
设计方案
需要确定26个明文字母与密文的对应关系以及15个字符位置的置乱关系。
明文1:abbcccddddeeeee 通过数量确定a-e的明密文对应关系,确定位[0],位[1-2],位[3-5],位[6-9],位[10-14] 块对应的置乱关系
【第一个明文确定a-e的映射与分块的置乱】
明文2:ffgfghfghifghij 通过数量确定f-j的明密文对应关系,每个位块中含有的明文均不重复,结合明文 1的初步结果可以得到所有位置的置乱关系
【第二个明文确定f-j的映射(与第一个原理相同),再确定分块内部的置乱对应关系】
明文3:klmnopqrstuvwxy 通过前两个明密文对,已经破译所有位置的置乱关系,可以直接得出k-y的明-密文对应关系,z的对应关系最后也可以得出。/
【对最后第三个密文反向置乱即得到映射的密文,反解即得到所有明文映射】
直接计算
n ≥ log2(26! + 15!)/log2(15!) = 2.196,即至少需要3个明密文对。
现代密码学理论
信息论基础
信息量与熵
信息量H(x)应当是事件概率p(x)的函数,满足:
- 是概率p(x)的单调递减函数
- 信息量H(x)非负
- 当概率p(x)=1时,信息量H(x)=0
- 独立事件的信息量是事件信息量之和
定义:随机事件x的信息量𝐻(𝑥) = − log 𝑝(x)
随机分布X(信源)的信息量(即信息熵):H(X) = - Σ p(x) * log p(x)
冗余
长度为N比特的消息M,假设它的信息量为H(M),则其冗余度为: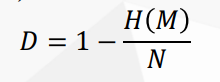
完美安全
完美安全含义:
- 窃听者截获的密文不能提供任何信息
- 完美安全的充分必要条件为:对所有的消息m和密文c,都有等可能的对应。
n个等概率消息,需要用n个等概率密钥来实现完美安全。此即一次一密。
密钥唯一解距离
唯密文攻击下,使H_c(K)接近于零的最小密文长度。
N_uk = H(K) / D
其中H(K)为信息量,D为消息的冗余度。
示例:对周期为d的置乱密码
H(K) = log d! ~= d*log(d/e)
冗余度为0.73.
则唯一解距离为1.4d*log(d/e)
Feistel结构分组密码
分组密码
分组密码(Block Cipher) :
- 通常以大于等于64位的数据块为处理单位
- 密文仅与算法和密钥有关,与明文数据块的位置无关
n比特的明文分组,加密产生n比特的密文分组
2^n个不同的明文分组,各自产生2^n个唯一的密文分组
- 本质上是一个巨大的代换表
完美安全的密钥需求
- n位的分组就有2^n种输入
- 每种输入需要n位“密钥”控制,确定映射到哪一个密文
- 共需
n × 2^n位密钥
加密算法结构
- 将输入等分为两段,进行若干轮运算,每轮中
- 对左半段数据进行代换
- 依据轮函数F(右半段数据和子密钥)
- 然后置换:交换左右两段数据
一个轮函数示例:
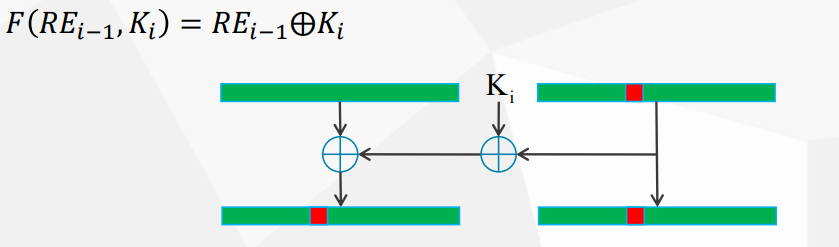
注意解密算法与加密算法过程相同,但子密钥使用的次序相反。
DES
雪崩效应:
- 明文或密钥的一比特的变化,引起密文许多比特的改变
- 加密算法的关键性能之一
- 希望明文或密钥的1比特变化,会使大约半数密文比特发生变化;否则,可能存在方法减小待搜索的明文和密钥空间
DES安全性分析
DES不能抵御差分分析、线性分析。
- 差分分析:
- 一种选择明文攻击
- 分析明文对的差分与密文对的差分之间的关系
- 确定轮运算的子密钥,从而恢复密钥比特
- 线性密码分析:
- 攻击16轮DES需2^43个已知明文
- 基本原理:寻找密码算法的有效线性近似表达式
- 建立关于密钥的方程组
中间相遇攻击
攻击双重DES,平均工作量仅为2^56
思路:寻找X = E[K1 , P] = D[K2 , C],即加密解密的中间态
3DES: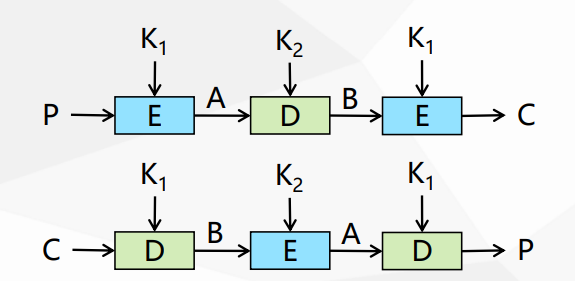
加密、解密交替使用,为了与单次DES兼容。
