所有学过高数的大学生都知道,如果在极限式中出现了乘除形式的等价无穷小(其实加减形式也可以用,但有条件),可以非常方便地直接替换化简。不过究竟是为什么呢?
课本上的描述很形象,因为两个无穷小在趋近于0时表现相同,所以可以替换,但让人更加迷惑,什么是表现相同呢?说到底,无穷小的阶到底是什么?更关键的问题在于:究竟如何求得一个表达式的等价无穷小。
等价无穷小的证明很容易:
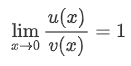
$$
\lim\limits_{x\to0}\frac{u(x)}{v(x)}=1
$$
求出这个比值极限,为1则说明是等价无穷小。例如:
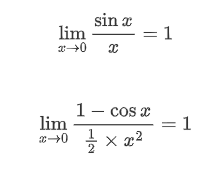
$$
\lim\limits_{x\to0}\frac{\sin\x}{x} = 1
$$
$$
\lim\limits_{x\to0}\frac{1-\cos\x}{\frac{1}{2} \times x^2} = 1
$$
也可写作:
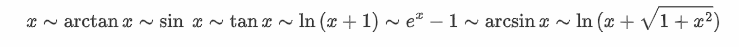
$$
x\thicksim\arctan x \thicksim \sin\ x \thicksim \tan x \thicksim \ln{(x+1)} \thicksim e^x-1 \thicksim \arcsin x \thicksim \ln{(x+\sqrt{1+x^2})}
$$
注意最后一个很常用。
但如果给出任意一个函数表达式,如何计算它的等价无穷小呢?
高数书上其实也已经给出了答案,就是用泰勒展开式计算。
所谓无穷小的阶,实际上是泰勒公式的余项精度差异。等价无穷小的定义:
$$
f(x) = g(x) + o(x)
$$
即无穷小等于其等价无穷小 + 高阶无穷小。移项得,两个等价无穷小相减,得到高阶无穷小,实际上是相同精度的泰勒公式相减得到更高精度的余项。
例如sinx的泰勒展开式:
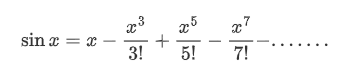
$$
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} - …….
$$
很容易发现,在泰勒公式精度为一阶时,展开为:
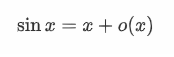
$$
\sin x = x + o(x)
$$
即x + x的高阶无穷小,因此x与sinx为同阶无穷小。
而在在同阶无穷小相减时,例如:

$$
x - \sin x = \frac{x^3}{6} +o(x^3)\qquad \qquad \quad \ \ \arcsin x=x+\frac{x^3}{6}+o(x^3)
$$
得到的就是泰勒展开式的下一项,因此有等价无穷小:
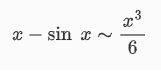
$$
x - \sin\ x \thicksim \frac{x^3}{6}
$$
所以实际上,一切等价无穷小替换的题目都可以用泰勒公式展开计算,而且永远不会碰到0 - 0,因为在等价无穷小中略去的高阶无穷小,都在泰勒展开式的余项中,继续展开计算即可。
