高等数学拾遗(上)

第一章 函数 极限 连续

函数是一切的基础，但与高中数学区别不大。

极限是最重要的难点，求极限是高等数学三大基本运算：求极限，求导，求积分的基础。

连续是根据极限定义的，对求导、求积分和微分中值定理都很重要。

函数

初等函数在其定义区间（注意：不是定义域内，因为可能定义域本身不连续）内一定连续。

初等函数定义：由常数和基本初等函数经过有限次的加、减、乘、除和复合所得到，且能用一个解析式表示的函数称为初等函数。

基本初等函数：幂函数，指数，对数，三角，反三角这五类函数。

极限概念

主要题型：

1. 极限概念性质与存在准则
2. 求极限
3. 无穷小量阶的比较

数列极限

$$
\lim\limits_{x\to\infty}x_n=a
$$

定义：对任意正数ε > 0，总存在正数N > 0，使当n > N时，恒有|x_n - a| < ε。

此时，在a的邻域(a-ε, a+ε)内，有无限多个数，但在这个邻域以外，只有有限个数。

注：

1. 数列极限与该数列的前有限项无关
2. 如果数列{a_n}的极限是A，则其任意子数列的极限也是A，例如{a_2n}和{a_2n-1}。（但反过来不成立，除非子数列相加为原数列）

数列极限经常用夹逼准则放缩求解。

函数极限

自变量趋近于无穷大时的极限 <==> 自变量趋近于正无穷极限 = 自变量趋近于负无穷极限

即暗含：左右极限均存在，而且相等。

对于以下三类函数，要特别注意是趋近于正无穷还是负无穷：

1. 1/x (+∞和-∞)
2. e^x (+∞和0)
3. arctanx （pi/2和-pi/2）

经常考察这三个函数的左右极限存不存在，此外还有分段函数当然也要考虑（理所当然的）。

极限性质

1. 有界性
2. 保号性

两个性质均有数列和函数两个版本。

3. 极限与无穷小的关系

有界性

数列：若数列收敛，一定有界。但反之不成立。

函数：若f(x)在x_0处极限存在，则函数在x_0某去心邻域内有界（局部有界性）。反之也不成立。例如sin(1/x)在x = 0处邻域有界，但这个函数在x = 0时极限不存在（为震荡间断点）。

保号性

数列：数列在n趋近于无穷大时极限为A

1. 若A > 0，则必存在正数N > 0，在n > N时，一定有x_n > 0。反之A < 0，则必有x_n < 0。
2. 反过来推导，若存在N > 0，当n > N时，有x_n >= 0，则有A >= 0。反之有x_n <= 0，则A <= 0。

注意：从极限推数列项时，必须是不等于0推不等于0。而反过来数列项推极限时，必须有等于号，否则不成立。

函数：f(x)在x趋近于x_0时极限为A

1. 若A > 0，则存在δ > 0，在δ的去心邻域里，有f(x) > 0。
2. 反过来推导，若存在δ > 0，在δ的去心邻域里有f(x) >= 0，则有A >= 0。

性质与数列一致，要注意极限推函数值时没有等于号，函数值推极限时有。

极限与无穷小的联系

f(x)的极限为A，则有lim f(x) = A + o(x)，即函数等于极限值加自变量的无穷小。

反过来也成立。

极限存在准则

1. 夹逼定理 => 多用于求数列n项和极限
2. 单调有界数列必有极限准则

无穷小

定义很简单，即极限为0。

性质：

1. 有限个无穷小的和是无穷小
2. 有限个无穷小的积也是无穷小
3. 无穷小与有界量(例如sinx)的积是无穷小(常用)

无穷大

无穷大量的比较：

*无穷大量与无界量的比较：

无穷大的关键定义是任意，无界量的关键定义是存在。

即当n > N时，恒有|x_n| > M为无穷大，而存在N使|x_N| > M为无界量。

无穷大量包含无界量。

求极限(重难点)

基本极限

$$
\lim\limits_{x\to0}\frac{sinx}{x} = 1
$$

$$
\lim\limits_{x\to0}(1+x)^{1/x} = e 或 \lim\limits_{x\to\infty}(1+\frac{1}{x})^x=e
$$

注意：这个基本极限的关键是底数域指数互为倒数，而且指数趋近于无穷，如果换成指数趋近于0，那么极限不存在。因为两个方向趋近，当趋近于0-时，底数趋近于负无穷，但指数函数，底数通常要大于0，因为负数的分数指数没有意义，所以极限不存在。

但如果改为趋近于0+，就可以很容易用洛必达求出来极限是1。

其他：
$$
\lim\limits_{x\to0}\frac{a^x-1}{x}=\ln a
$$

$$
\lim\limits_{n\to\infty}{\sqrt{n}}^n=1
$$

$$
\lim\limits_{n\to\infty}e^{nx}=0(x<0);
\lim\limits_{n\to\infty}e^{nx}=+\infty(x>0);
\lim\limits_{n\to\infty}e^{nx}=1(x=0)
$$

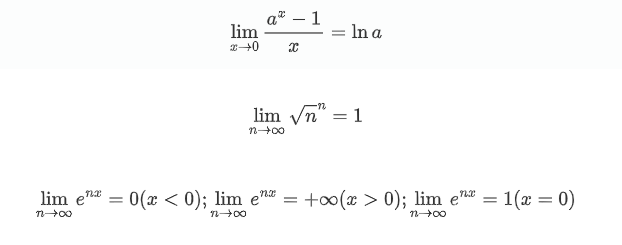
最后面这个最常用。

基本公式变换

立方和公式
$$
a^3+b^3=(a+b)(a^2+b^2-ab)
$$
立方差公式
$$
a^3-b^3=(a-b)(a^2+b^2+ab)
$$
立方累加公式：
$$
1^3+2^3+3^3+…+n^3=(\frac{n(n+1)}{n})^2=(1+2+3+…+n)^2
$$

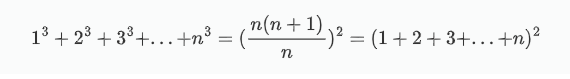
这个是最神奇的，自然数立方和累加，居然等于自然数等差数列累加的平方。搜了下网上的证明大部分也都是数学归纳法的，没有直接的证明。

平方和：
$$
1^2+2^2+3^2+…+n^2=\frac{n(n+1)(2n+1)}{6}
$$

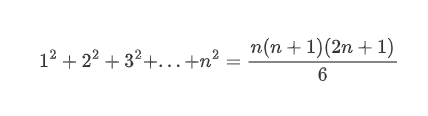
1^∞型极限

一般两个思路：

1. 凑基本极限的e
2. 变形+洛必达

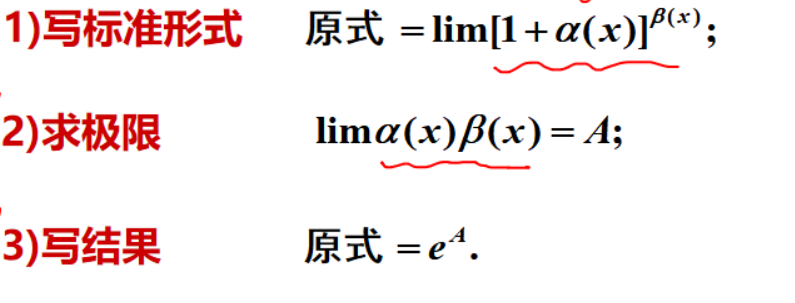
这个结论，通过等价无穷小替换很容易推得。

等价无穷小替换

原则：

1. 乘除关系都可以替换
2. 加减关系替换需要符合条件：相减时，替换后的两个极限不能等价（即相除求极限不等于1）；相加时，相除求极限不等于-1.

实际上就是替换之后不能为 0 就可以换，因为为0时相当于忽略了高阶无穷小，会损失精度。

等价无穷小替换的本质是泰勒公式，详见具体推导。

常用等价无穷小：

有理运算法则

这个是计算极限的基本，但很容易犯错。

关键是：如果可以拆成加减或者乘除求极限，拆出来的极限必须存在。

注意：当加减形式拆出来的极限为无穷大时，不能拆，会损失精度（此时需要继续做洛必达或其他变换）。

因为如果拆出来的极限存在，而且要计算的极限一定存在，所以被拆之后的部分极限也一定存在。反之就算整体极限存在，其中拆出来的部分不存在，被拆的也有可能不存在 => 此时不能拆开计算。

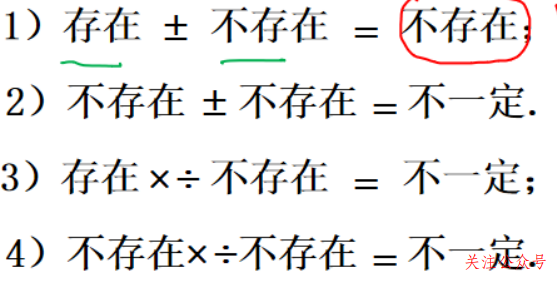
上面的结论对极限、连续、可导均成立，即只有存在与存在经过加减运算后也存在，其他都不一定。

推论：

1. 极限非零的因子，可以先提出计算（即计算时要时刻观察有没有可以直接求出来的部分简化）。
2. 若f(x)除g(x)的极限存在，且g(x)极限为 0，则f(x)极限一定为 0.
3. 若f(x)除g(x)极限存在且不为0，且f(x)为 0,则g(x)极限一定为 0。

洛必达法则

使用条件：分子分母均在x_0某去心邻域内可导，且上下求导后的极限存在（或极限为∞）。

泰勒公式

常用泰勒公式：

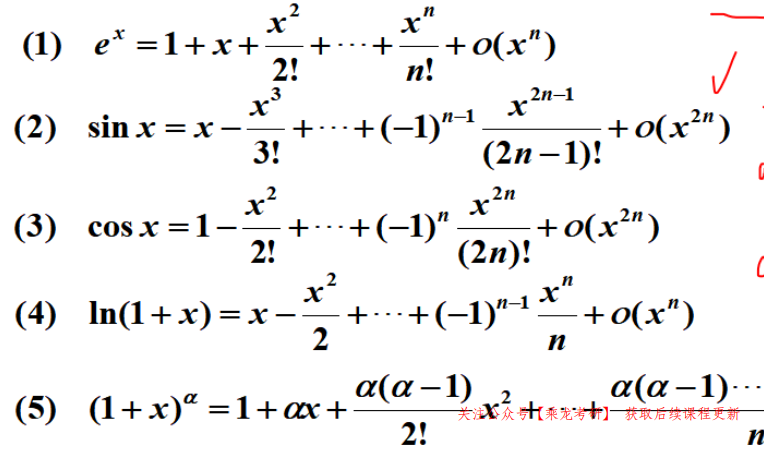
（6） arctanx = x - (1/3)*x^3 + (1/5)*x^5 + …..

使用泰勒公式时，要展开的项数是由最高指数决定的，因此后面的高阶无穷小忽略即可。

注意：计算时，使用泰勒展开加减要注意展开阶数，直到不能被完全消去。多展开的高阶部分可以直接舍去。

无穷小运算定理：

1. n阶无穷小与m阶无穷小相加，且n<=m，此时结果为n阶无穷小
2. n阶无穷小与m阶无穷小相乘，结果为 n+m 阶无穷小
3. x^n乘m阶无穷小，结果为x的 n+m 阶无穷小（注意）。

因此高阶无穷小可以直接舍去。

泰勒公式求法

1. 直接使用定义
2. 四则运算
3. 复合
4. 逐项求导/逐项积分（例如arctanx导数很容易求泰勒公式，对结果逐项积分即得到arctanx的展开式）

定积分定义求极限

当表达式可以提取出1/n时，可以凑定积分定义求解极限。

定积分标准定义为Σf(psi)*Δx在Δx最大的值趋近于0时的极限，可以拆分为(1/n)*Σf(psi)*(b - a)，凑这个值即可。

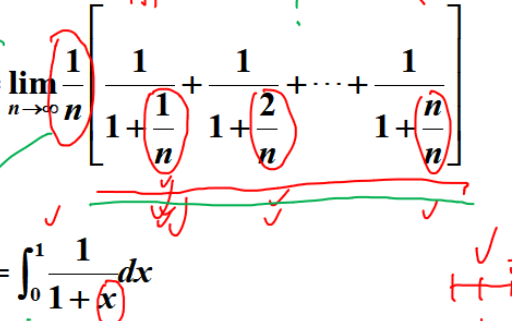
某些凑定积分定义的极限也可以用夹逼准则求，多半要用到基本不等式：

x/(x+1) < ln(x+1) < x (x>0)

连续

f(x)在x_0处的极限，与f(x_0)没有关系，但如果f(x)在x_0处连续，就有极限等于f(x_0)。

间断点

定义：函数在x_0的某去心邻域有定义，但不连续，称x_0为间断点。

分类：

• 第一类间断点：

1. 可去间断点：左极限 = 右极限
2. 跳跃间断点：左极限 ≠ 右极限

• 第二类间断点：左右极限至少有一个不存在

无穷间断点，震荡间断点(但不是只有这两种，例如sin(1/x))。

第二章 导数与微分

难点：

• 利用导数定义判断可导性
• 求高阶导数

导数

定义：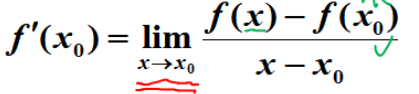

其中f(x)是动点，不能直接赋值，需要代表达式；f(x_0)是静点，可以直接代值。

注意：由可导可以推出上述定义式，但由定义式还不能直接推出可导，而必须要满足：

1. x(或x表达式)趋近于x_0
2. x不等于0
3. 关键：x必须从两个方向趋近于x_0，即要趋近于0+和0-。

注意：

1. 对数列极限，n趋近于无穷，即n趋近于正无穷。
2. 如果给出的两个表达式为两个动点，则一定不存在，极限定义必须是一动一静。

可导

• 可导 <=> 左右导数均存在，且相等。

• 连续不一定可导(例如|x|在x=0处连续，但不可导)，可导一定连续。

• 不可导不一定没有切线。例如根号下x的绝对值，在x=0处不可导，但有切线(y轴)，因为两侧导数值刚好为+∞和-∞。

对含绝对值函数的常用结论：对f(x)=φ(x)|x-a|，若φ(x)在x = a处连续，则f(x)在a可导的充要条件是φ(a) = 0。

可导抽象函数与洛必达

注意：已知f(x)有n阶可导，则说明洛必达最多可以对f(x)n-1阶求导，即f(x)n阶可导，推不出f(x)的n阶导函数连续，也推不出f(x)n阶导函数极限存在。例如x^2*sin(1/x)，且x = 0时为0.这个函数处处可导，但导函数在x趋于0时的极限不存在（当然也不连续）。

但如果已知f(x)有n阶连续可导，则f(x)可求n阶导。

导数性质

• f(x)为奇函数，则f(x)的导数为偶函数。

• f(x)为偶函数，则f(x)的导数为奇函数。

• f(x)为周期函数，则导数也为周期函数(周期相同)。

• 复合函数，若内函数可导，外函数可导，则复合函数也可导。

反函数求导

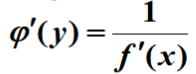
要注意是谁相对于谁的函数。

参数方程求导

上下同时对t求导即可。

注意：求dy/dx不容易错，但求d^2y/dx^2容易错，一定注意是对x求导还是对t求导，如果对x求导一定要乘一个dx/dt，如果是对t求导要乘dt/dx。

也可：将参数方程求导转为复合函数求导。

隐函数求导

始终记住：y是相对于x的函数，对表达式两边对x求导。

对数求导

对连乘连除开方形式的求导，多用先取对数将乘变成加再求导（表达式两边取ln，再两边求导，让左边为y’/y）。

注意：lnx求导为1/x，同时ln|x|求导也是1/x，所以绝对值不影响结果。

微分

定义：dy即Δy的线性主部,dy = AΔx。

可导一定可微。

导数与微分的区别：

1. 导数是函数在某点的变化率，微分是函数在某点变化量的近似值。
2. 几何意义：导数是函数在某点的切线斜率，微分是函数曲线在某点切线上的增量。

高阶导数

f(x)在x_0处n阶可导，则函数在x_0的邻域内必然有一切低于n阶的导数。

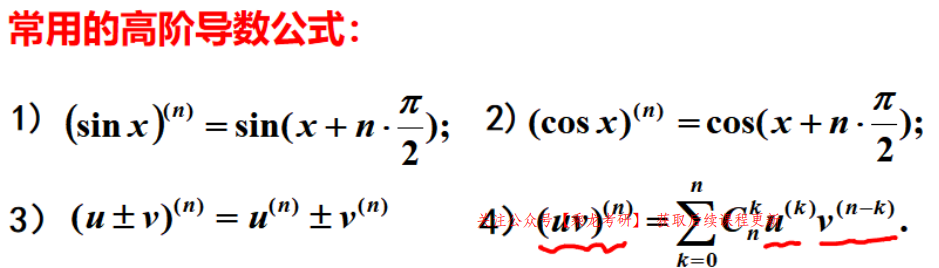
注意(uv)的n阶导数形式为牛顿二项式，即C(k,n)*u^(k)*v^(n-k)。

但是一般不会求到k阶，因为如果有u，v中有幂函数，在求到次数+1时为0，此时之后的部分全为0，若求在0的值时，此时公式(例如次数为2时)变成C(a,n)u^(2)*v^(n-2)。

在求高阶导数时，一般要求一阶，二阶，三阶然后找规律：关键在于对复合函数求二阶时，不要忘记乘上对复合内函数所求导数的平方（相当于对一阶导数求导后，再乘内函数的导数再乘之前的乘因子）。

相关变化率

已知一个变化率，求另一个与之相关的变化率。

关键是建立变量间的联系，然后类似参数方程求导，搞清楚对谁求导即可。

第三章 微分中值定理及导数应用

微分中值定理

费马引理：

f(x)在x_0处可导，且在x_0取得极值，则f(x_0)的导数=0。

三大中值定理

罗尔定理：

条件：

1. f(x)在[a,b]连续
2. f(x)在(a,b)可导(开区间连续，闭区间可导)
3. f(a) = f(b)

则存在a属于(a,b)，使f(a)导数为0。(即存在一点，使该点切线平行于x轴)

拉格朗日中值定理：

条件：(开区间连续，闭区间可导)

区间内存在一点，使该点切线平行于端点连线。(即罗尔定理的推广)

柯西中值定理：

即参数方程的拉格朗日中值定理：

意义

建立了函数与导数的联系

关系

柯西是拉格朗日的推广，拉格朗日是罗尔定理的推广。

应用

罗尔定理多用于和零点定理共同处理方程根的存在问题。

根的个数多用单调性判断。

泰勒公式

常用于研究f(x)的n阶导数。

意义：使用多项式函数逼近复杂函数；建立函数与高阶导数的关系。

区别：

1. 皮亚诺余项为局部泰勒公式，主要研究极限和极值。
2. 拉格朗日余项研究函数整体。主要研究最值和不等式。

基本泰勒公式：

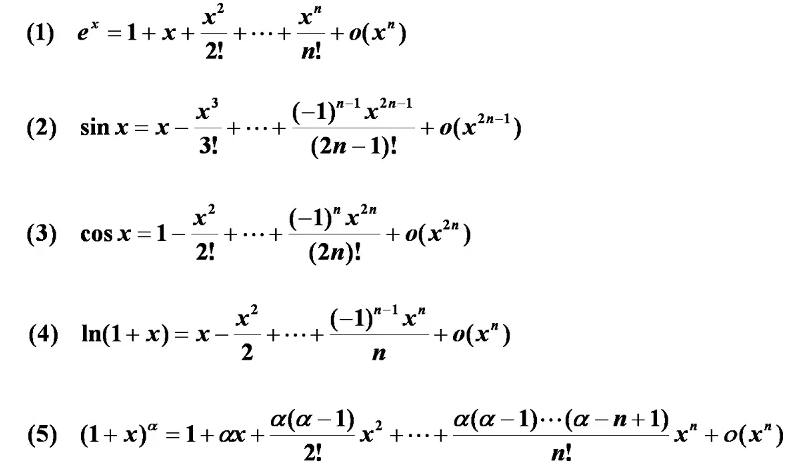
导数应用

技巧

判断极值的主要思路：

1. 求某点的左右极限(左右导数)
2. 定义判断极值：定义计算某点极限值，再比较两侧邻域
3. 利用几何意义画图，尤其是多项式函数时

注意：应用时建模，如果函数很复杂难以求导，可以换种思路(换个自变量建立函数)

单调性

开区间内导数>0，则函数在闭区间内单调递增；反之则递减。

极值

必要条件：若可导函数f(x)在x_0处可导，且在x_0处取到极值 ===> f(x)` = 0

此时称导数为0的点为“驻点”。

极值与驻点

1. 极值点不一定是驻点，例如|x|在0取得极值，但不是驻点(在x=0时不可导)。
2. 驻点也不一定是极值点，例如x^3在x=0是驻点，但不是极值点。

若f(x)可导，则极值点一定是驻点。

极值点只可能在两处存在：驻点和导数不存在的点。

凹凸性

二阶导数为大于0，则曲线为凹；二阶导数小于0，则曲线为凸。

拐点判断与极值点类似。

渐近线

水平渐近线：求x趋于无穷的极限，极限存在且不为无穷时有水平渐近线

垂直渐近线：求x趋近于无穷的极限，极限为无穷时，为垂直渐近线

注意：要特别注意e^x对正无穷和负无穷极限不同，前者为正无穷，后者为0(水平渐近线)

斜渐近线：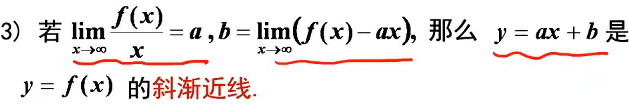

斜渐近线判断：如果函数可以写成一个线性函数加上一个在x趋近于无穷时等于0的函数，则渐近线就是这个线性部分。如果趋近于无穷时极限为常数，则渐近线就为线性部分加这个常数。

曲率

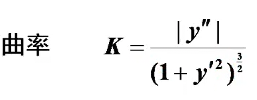
曲率半径：曲率的倒数

（图一乐）边际函数与边际分析

第四章 不定积分

概念

原函数存在定理：

1. 若f(x)在区间上连续，则一定存在原函数。
2. 有第一类间断点的函数，一定没有原函数
3. 有第二类间断点的函数，也可以有原函数

求积分

三种主要方法：

1. 第一类换元：凑微分
2. 第二类换元：

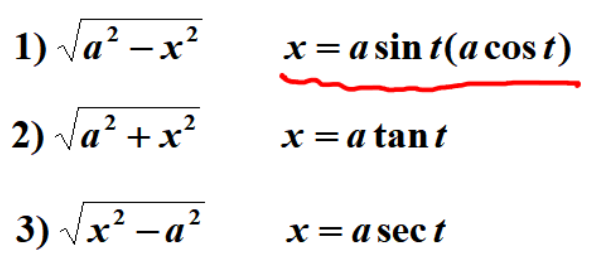
注：对含有*sqrt(e^x+1)*形式的积分，也可以直接换元为t。

3. 分部积分：主要有以下三种分部方式

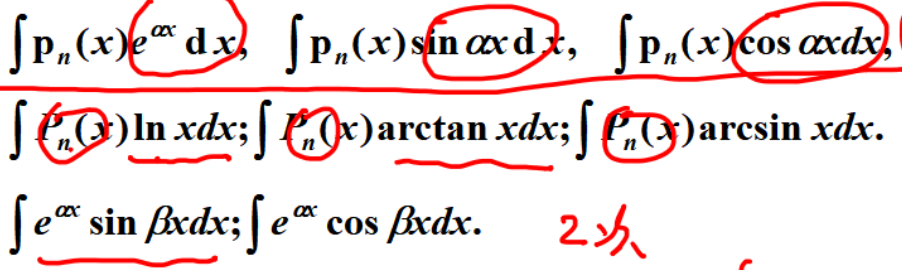
三种对应三种计算方式：

• 对幂函数与e^x和三角函数的乘积，需要让幂函数一直降低次数，因此让另一部分作为被积分部分
• 对幂函数与lnx和反三角的乘积，后半部分比较容易求导，所以让幂函数作为被积部分
• 第三种是最复杂的，但计算最容易，让两个部分分别作为被积分部分，然后凑出原本形式解方程即可。

三种积不出的函数

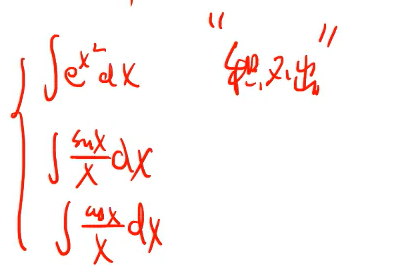
遇到这种需要换方法，例如二重积分时，遇到要由x型换成y型计算。

三种常见求法

有理函数求积分

碰到这种复杂有理分式求积分，可以使用一般方法分解成几个有理部分：

分母有两部分，分别是一次的x-1和二次的x^2+x+1，但x-1乘了两次，所以是二重的一次部分。

所以拆成如上三部分，两个x-1都是一次，所以分子降次为0次，设为常数。x-1出现了两次，所以有一个x-1和一个(x-1)^2，然后二次的分子就是一次式，设为一般式kx+b。

三角有理式积分

判断积分式相对于sinx和cosx的奇偶性，整体正负由sinx决定则凑dcosx，反之则凑dsinx。

若均为偶则凑dtanx.

简单无理式积分

对于根号内为一次多项式，直接整体换元：

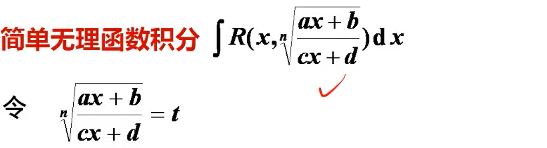
常见题型

求分段函数不定积分

需要注意分界点的连续性，一般由两种求法：

1. 设两边原函数为F(x)+C1和G(x)+C2，然后根据两边在分界点相等求出C
2. 直接求变上限积分作为原函数

求一般积分

(1/x^2-1)这个式子经常出现，要注意是可求积分的，原函数是1/2 * ln(|x-1|/|x+1|)。

第五章 定积分

定义与概念

定积分是和式极限：分，匀，和，精确

注意：

1. 定积分定义的区间关键在任意划分，所以取极限是λ趋近于0，即划分区间的最大值趋近于0，而不是分成的区间数n趋近于无穷，二者不等价(前者可以推出后者，反之不行)。
2. 定积分仅与f(x)和[a,b]有关，即函数与区间。
3. 极限值与区间分法和点取法都无关

3的推论：因为与分法无关，所以可以取最简单的等分方便计算：

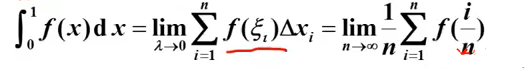
这里与前面凑定积分定义的求极限法一致。

这个很常用，关键在提取出可爱因子1/n，然将1/n….n/n的部分看作x

定积分存在条件

充分条件：

连续一定可积。

必要条件：

可积一定有界，有界不一定可积(例如迪利克雷函数)。

注意：可积一定有界仅适用于闭区间。开区间不一定有界，例如对lnx在0到1上的定积分为-1，但lnx在(0,1)无界。

性质

不等式性质：

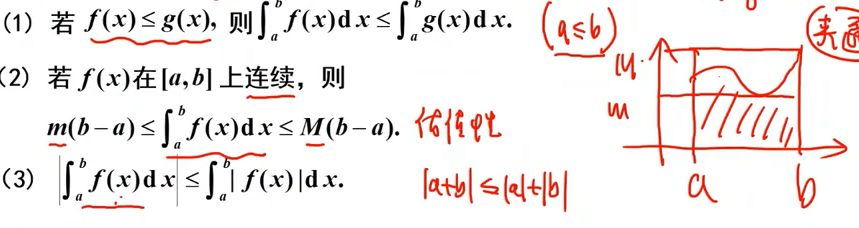
其中第二条最常用，即定积分大小介于函数最大值和最小值乘区间大小之间，右边的几何定义很容易说明。

中值定理

若f(x)连续

由微积分基本定理和拉格朗日中值定理很容易证明：F(b) - F(a) = F`(k)*(b - a)

变上限函数积分(*很常考)

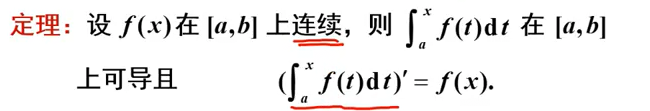
意义：

1. 联系起微分和积分的运算：互为逆运算
2. 连续函数一定有原函数

注意：变上限积分的导数是函数本身，但反过来不是 ===> 函数导数的变上限积分不是函数，而是直接求定积分：
$$
\int_{0}^{x} f’(t) dt = f(x)-f(0)
$$
即已知函数导数，对其求积分得到函数时，需要知道一个常数参数的函数值（否则有多种原函数）。

推论:若f(x)连续

1. f(x)为奇函数，则在0到x上的变上限积分为偶函数
2. 反之f(x)为偶函数，则其变上限积分为奇函数

计算方法（重要）

• 当dt的变上限积分中出现了x，由两种思路：

1. 将x作为t的函数中的常数，提取出来单独计算
2. 换元，将x-t换元为u计算，则du = - dt

• 上下限分别为x的函数时，计算变上限积分的导数可直接代入当作复合函数求导计算，即结果形如f(x^2)*2x - f(e^x)*e^x。
• 分段变上限积分：

讨论正负号时要仔细考虑积分区间，例如下题

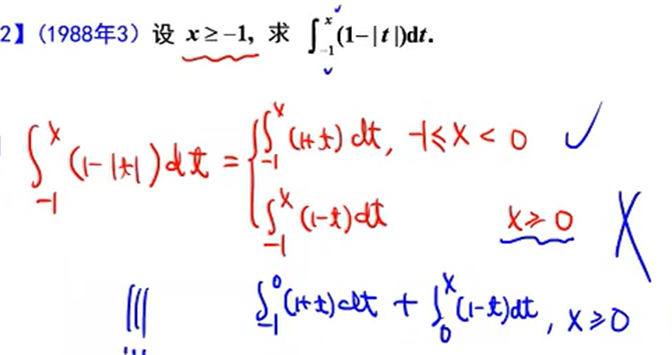
将-1到x的区间分为-1到0与0到x计算，否则会出错。

• 对0/0型，一般有两种思路：换元+洛必达 和 积分中值定理（尤其在积分区间为0到x，且x趋近于0时很常用，因为kesi是定值0）

定积分计算方法

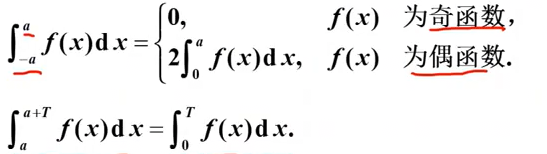
如果被积函数是由奇函数和偶函数组成，且积分区间对称，那定积分直接计算2*一半积分区间即可。

几何意义：

1. 形如sqrt(a^2 - x^2)的定积分，可以是化为单位圆面积计算，在0到a上积分结果为(pi/4)*a^2
2. 形如sqrt(2ax - x^2)的定积分，在0到a上结果也为(pi/4)*a^2

基本定积分公式(常用)

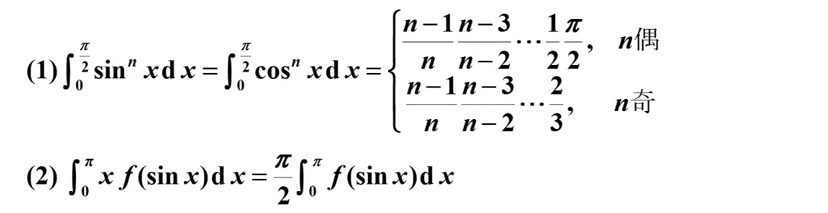
这两个都很常用，尤其第一个凑出0到pi/2的积分区间后计算很方便。

反常积分

上面的定积分都满足两个条件：

1. 积分区间为闭区间，例如[a,b]
2. 函数有界

由此可得两类反常积分：无穷区间和无界函数。

无穷区间反常积分

定义：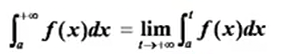

与一般定积分不同，不是和式极限，而是趋近于无穷的极限。当这个极限存在称为收敛，反之为发散。

敛散性判别法

与无穷级数的敛散性相似。

比较判别法

大的反常积分收敛 ==> 小的收敛

小的反常积分发散 ==> 大的发散

比较判别法的极限形式

将要判断的函数作比值再取极限：

注意常用结论：P级数的敛散性

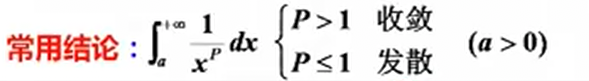
P级数常作为无穷区间的反常积分判断敛散性比较的对象。

无界函数反常积分

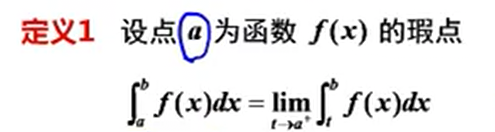
如上定义是边界是无界的情况，也有在积分区间中有无界：

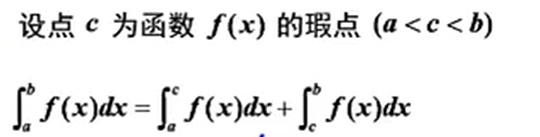
此时必须两个定积分都存在，才能称为反常积分收敛。

敛散性判别法

与无穷区间的情况一样，关键在P积分。

但是比较的级数与之不同：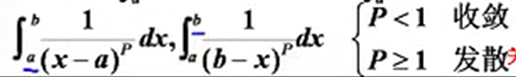

并且收敛和发散也相反，这个p积分是在p<1时收敛的。

常见题型

对形如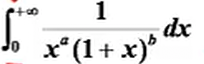的积分，包含两种反常积分：在0时是无界，在+∞时是无穷区间，因此判断敛散性时需要拆成两部分，才能使用上面的比较判别法判断，例如拆成0到1和1到+∞(实际上还是判断0和正无穷，所以与1无关)，再单独构造P积分比较即可。

第六章 定积分应用

几何应用

平面图形面积

实际上这两个公式都可以利用二重积分计算面积。
$$
S=\iint_{D}1\ dx
$$

旋转体体积

与上面类似，都可以用累次积分推得。

曲线弧长

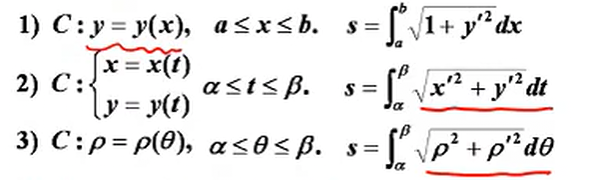
实际上也是由下面推得：
$$
ds=\sqrt{1+y’^2}·dx
$$

物理应用

主要有三部分：

1. 压力
2. 做功
3. 引力(很少考)

关键是利用微元法分析变量，构造x+dx和x的薄片再求定积分。

第七章 常微分方程

基本概念

定义：含有未知函数导数/微分的方程称为微分方程

阶：含有未知函数导数的最高阶

通解：含有独立任意常数个数等于微分方程阶数的解

特解：通解 + 初始条件可定下通解中的任意常数，此时称为特解

积分曲线：微分方程的解对应的曲线

一阶微分方程

可分离变量的方程

y’=f(x)*g(y)

即dy/dx=f(x)g(y) => dy/g(y) = f(x)dx

再对两边求积分即可得到解。

对y’=f(ax+by)形式的微分方程，可直接换元u=ax+by，再观察形式代入把du=a+by’的y’代入，即可化为关于u与x的可分离变量的微分方程求解。

齐次方程

齐次：各项次数相等(例如均为1)

例如x^2 + y'*x + y*x = y^2

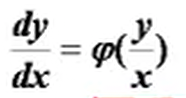
求解时，换元u=y/x，再对将du分解开，即可划为可分离变量的方程

线性方程

要求：

• 未知函数及其各阶导数都是一次幂。
• 未知函数及各阶导数的系数只能含有自变量或常数。
• 不能出现未知函数及各阶导数的复合函数形式。

y` + P(x)y = Q(x)

求解时代入通解公式：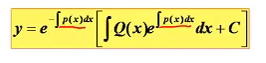

注意公式中的Q(x)没有求积分，而是直接乘进去整体求积分，这点容易搞忘。

当凑不出如上线性形式时，可以将x换为y的形式：
$$
x’ + P(y)*x=Q(y)
$$
通解公式也是类似形式。

伯努利方程

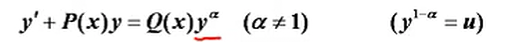
全微分方程

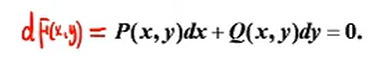
求解多用多元微分。

关键在凑微分：一般使用分组方式凑，例如可以将ydx+xdy凑为d(xy)，然后划为d(f(x))=0 –> f(x) = C的形式。

可降阶方程

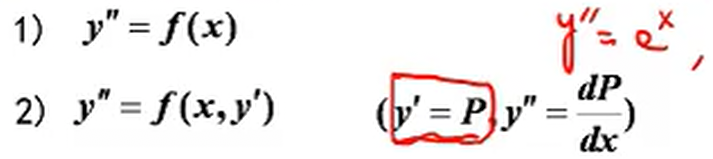
第二种形式中，只有二阶导和一阶导而没有y(不显含y)，此时可以将二阶方程转为一阶：令y` = P

不显含x时也可以换元降阶：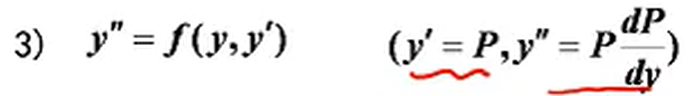

这种形式设y’为P，然后对y’求导化为P与y的函数，即可将二阶微分方程化为P与y的一阶微分方程。

求出来之后再将y’代回原式，即可化为y与x的可分离变量的微分方程。

注意：在利用通解和初始条件定特解时，求出一个常数就利用条件定下来，然后再求其他常数比合并常数一起求更方便。

线性微分方程解的结构(*)

齐次方程通解 = 两个线性无关特解的和

非齐次方程的通解 = 对应齐次方程的通解 + 非齐次方程的特解

如何判断线性无关：y_1(x)/y_x(x) != C

注意：由两个非齐次方程的特解，可以求对应齐次方程的特解 ===> 非齐次特解的差 == 齐次特解

解释：

1. 非齐次线性方程组的解 由 特解，齐次通解构成

2. 齐次通解由基础解系和系数构成

3. 相同的基础解系对应相同的特解

4. 同一方程组的基础解系是可以相互转化的

这样两个解一减就消掉了特解

常系数线性微分方程

实际上只能求这种的通解，很常用(*)。

齐次

利用特征方程：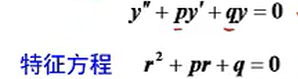

此时解有三种情况：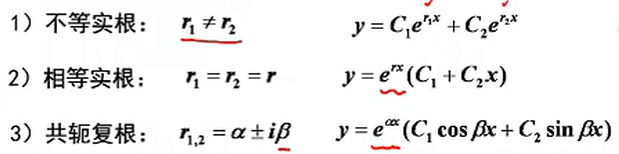

当有三阶或四阶时，有更多的根，将所有根对应的方程通解加起来即可。

非齐次的特解

利用待定系数法求特解：公式中的α和β是上面齐次方程特征根中共轭负根时的两个参数。

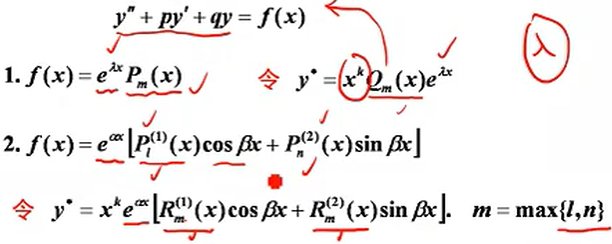
其中P_m(x)代表x的m次多项式，x^k要不要乘，取决于λ：如果λ是齐次方程的k重根，则需要乘x^k，如果为单根，则乘x，如果不是根，则不乘(即x^0)。定好Q_m(x)形式(一般是ax+b)后，代入原式即得具体特解。

第二种，判断x^k取决于α+iβ。如果α+iβ是齐次方程特征方程的一个根，则要乘x.

利用非齐次项，设出待定的特解，再与齐次的通解相加即得非齐次的通解。

(其中y*为非齐次方程的特解，这个其实直接看出来或者试出来也可以)

欧拉方程

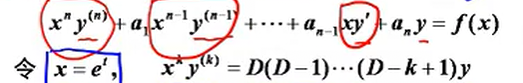
求x的次方与y的阶数有规律变化的方程根，换元x=e^t即可。

换元成D算子形式后，可直接将D换为r，即得对应齐次微分方程的特征方程。

积分方程

两边求导即可化为微分方程。

若不好求导，可换元为u=x-t再求导。